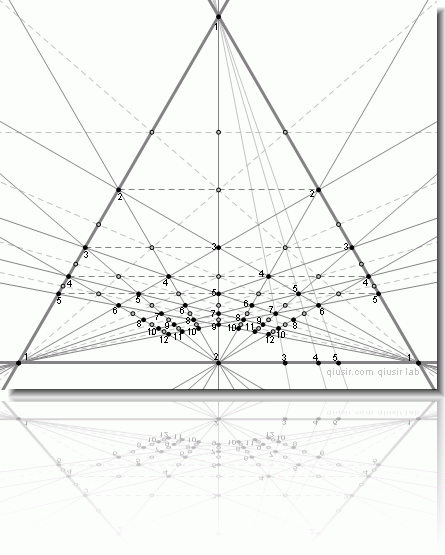
利用物理学中杠杆平衡原理求重心...可以形象建立GLaD的分割模型，以及作一些推广。
横看成岭侧成峰，远近高低却相通

只要三个顶点质量比值为整数...应该是一个很好的数学物理综合的范例。
专题探究
单纯从数字上[每个数字都是经过该点线段的等份点]就有“横看成岭侧成峰”的规律；而所有的数字又都彼此关联；如果看作是质量数的话，所有点都是相关图形的重心。[对角线交点就是重心的四边形的特征是？]

数学不是科学，但他的确奇妙。不数学是上帝的科学。
---------------------------------------
update:2004/6/17姜平无意中发现我的观点竟然和“质点几何”学很相近，我的懊恼换来他的安慰和鼓励。数学再发现：）有时间好好研究一下。不过至少证明自己的“发现”不是毫无意义，历史的巧合也落在我身上。

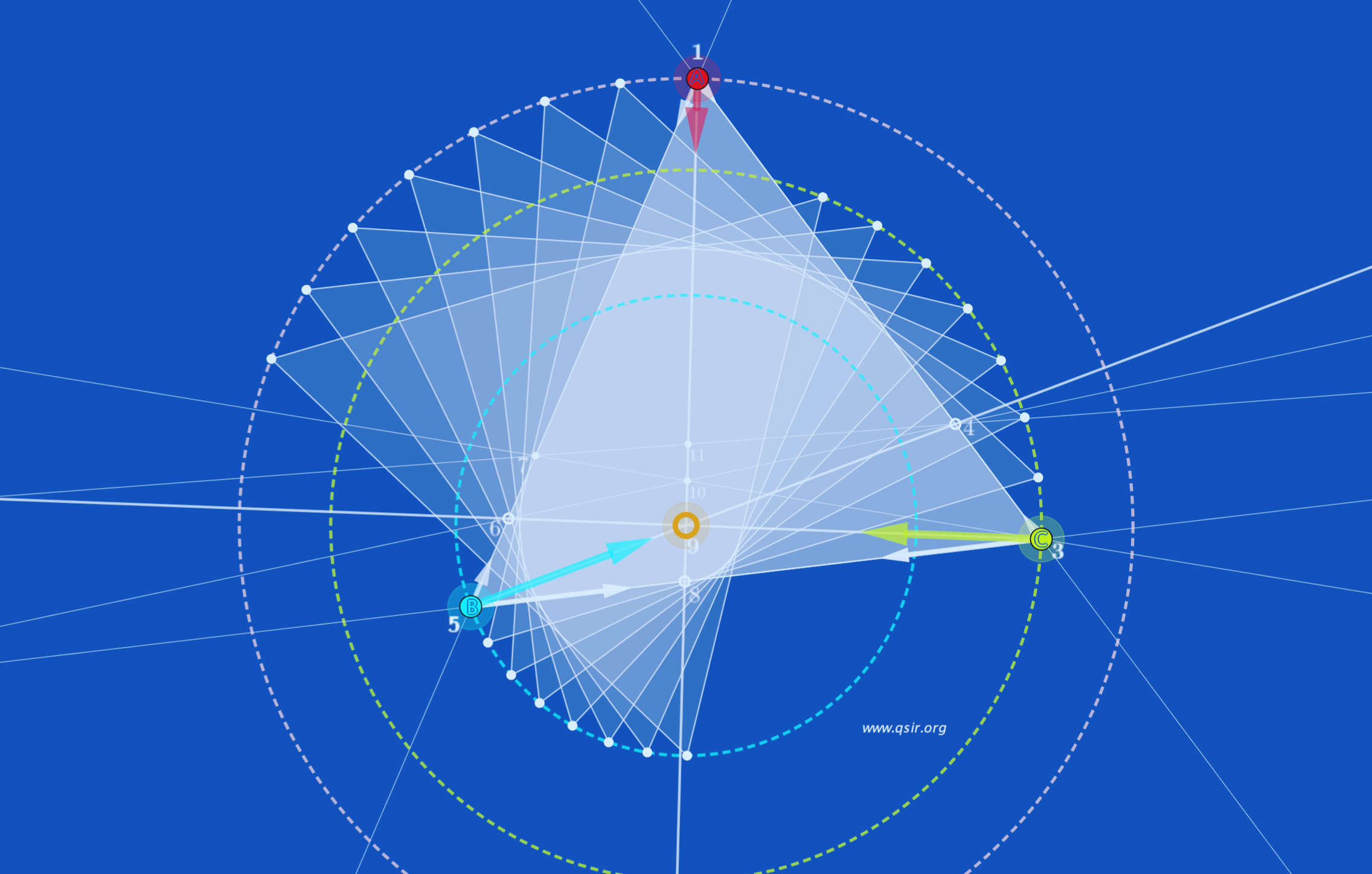
update(2018.11.25):
昨晚和学生讨论三星的一道题目，忽然觉得可以借用双星的质心概念（L^3/T^2=G(M+m)/4pi^2）方便来确定三星旋转中心的题目。尝试一般的三角形条件下...大半天的没课，大清早爬起来继续测试...

只要是满足相互作用，三个质点的引力必过一点，即便是不满足平方反比。而位置关系是正三角形则一定符合三星的稳定状态，而且可以把双星的结论迁移过来，利用质心的概念确定旋转中心。同时，很久之前探讨过的质点几何分割在这里也相遇了。

点赞的和阅读的不是发布的目的，主要还是自我讯息的记录。因为能重复一下上面的结论的似乎没有，更不要说有自己的新的想法了。忙着学习的事没时间学习...

On this day..

• 邻居家的月季花 - 2022
• 媒体 一个不良心态的家长 - 2004
• 告知与提问式教学并非有效的教学 - 2004