三 20
不经意看到善科网上的这篇文章(桥梁、弦艺术和Bézier曲线[?],英语原文[?]),除了被耶路撒冷弦桥(erusalem Chords Bridge)的艺术特质所感染,同样被缆线的纵横所吸引,对桥弦包络(缆线边缘的轮廓)的曲线好奇...
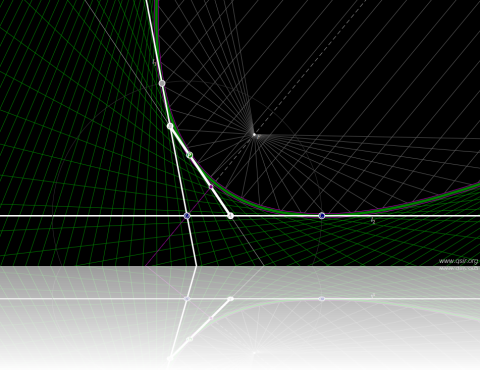
把这样一件复杂的实体抽象出一个平面的模型,我最先想到的是以前多次构造过的定长杆滑动的范例[?],一度以为那包络线和文章里提到的同属。一方面数学班张潇勇等同学(程同学和鲜同学同样有参与)给出了代数式,非抛物线,另一方面通过抛物线的光学特性反正,才意识到这是非常不同的两个模型...
构造从相互垂直的两直线上的点到交点距离和相等开始,中间尝试了多种方法,又把线段的包络拓展到直线的包络,后来发现要实现完整的抛物线包络,需要加入距离差为常数,再后来借助点的坐标值引入了比例,再把直线拓展到任意夹角,在用同样的比例在线段上缩放(考虑多阶贝塞尔曲线构制)...
O为两直线的交点、CO为定长、AO+BO=CO/AO-BO=CO\P分线段AB的比例同A分线段OC的比例,也同线段AB上另一点分BA的比例...
一些很表象的结论:包络线是抛物线;角平分线是对称轴;抛物线与两直线的切点在以和与差定值为半径的圆周上;以同样的比例在线段上两个端点分别为中心缩放的点,轨迹要么是抛物线上的点,要么是抛物线对称轴上的点...
立体到平面本就失去很多信息,次模型也没有考虑到力学等因素,甚至没有给出计算和证明,但这不妨碍我们从另一层面探究和发现:
比如椭圆和双曲线是平面上到两定点距离和与距离差为定值的曲线(以前讨论过距离平方和与差的题目),那上述的模型无非是两相交直线上风别两点与交点的距离和与差相等的曲线,而很有趣的是,原来的定长杆在墙角滑动的模型即等棍模型无非是直线上到交点距离平方和为定值,那么自然会想到距离积距离商为常数,如果直线变成圆弧...
也发现经常使用的keynote上图形绘制工具提供的竟然是贝塞尔曲线[?],而借用同比例回归到定长杆模型中,也会有不少新的认识...
☆直线上到交点距离和&差定值点的连线包络ChordsBridge~ (5549)


3月 22nd, 2013 at 15:36
选修课童鞋发先三角形周长定比分点的轨迹?中点的轨迹?
3月 22nd, 2013 at 15:46
和底边定同比分点的轨迹是抛物线,三角形周长中点的轨迹不同,但非常接近,很好奇非中点的定比分点的轨迹是什么样的曲线系?
3月 22nd, 2013 at 15:54
比例为k的定比分点轨迹和比例为1-k的轨迹交点在角平分线上...
5月 11th, 2013 at 09:19
qiusir,问一下,贝塞尔曲线是哪个点运动时,哪个点形成的轨迹?
5月 13th, 2013 at 09:32
维基百科上有,再,定比例初始的点...
5月 24th, 2013 at 14:44
http://zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A
8月 16th, 2019 at 14:27
你学到的知识,就和生活关系的层面上看,最先也是最容易接触的不是物理,而是数学...