四 02

动能也能“相对”······

教学|〖基础物理〗 金庆辰 2025

JQX/进取芯 小教研第一期（2025.3.27）

一、源起
2023年夏天，J的学生在讨论一道题目时提出一个相对动能的概念。题目如下：
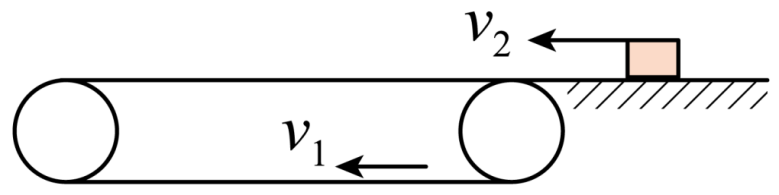
如图所示，一水平方向足够长的传送带以恒定的速度 v_{1} 沿顺时针方向转动，传送带右端有一个与传送带等高的光滑水平面，一质量为 m 的物体以恒定的速率 v_{2} 沿直线向左滑上传送带后，经过一段时间又返回光滑水平面。则在整个运动过程中，传送带与物体摩擦生热为？

正常通过v-t图像进行计算，也能很快求出相对路程，进而计算生热：
当 v_1 = v_2 时： Q = f \Delta d = 2mv_1^{2}
当 v_1 < v_2 时： Q = f \Delta d = \frac{1}{2}m(v_1 + v_2)^{2}
当 v_1 > v_2 时： Q = 2mv_1v_2
这三个结论都存在一个非常有趣的共性：
如果定义小物块相对传送带的动能为： E_k = \frac{1}{2}m(v_r)^2 （v_r为小物块相对传送带运动速度），那么 Q = \frac{1}{2}m(v_1 + v_2)^{2} - \frac{1}{2}m(v_1 - v_2)^{2}
想对本结论进行拓展，却发现只适用于水平传送带，斜传送带并不满足。那么，这是一个巧合，还是存在内在逻辑？让我们慢慢道来。

二、碰撞系数与非弹性碰撞消耗机械能
1. 碰撞系数
牛顿从实验中总结出一条规律：碰撞后两球的分离速度 (v_2 - v_1) 与碰撞前两球的接近速度 (v_{10} - v_{20}) 成正比，即e = \frac{v_{2} - v_{1}}{v_{10} - v_{20}} 。对于弹性碰撞e = 1
这里有一个有意思的结论：弹性碰撞前后，两物体速度差的绝对值相等。倘若我们将碰撞时间延长，或者等效为两个小球中间连接一个理想弹簧来放大碰撞过程，便可以得到黑板右侧的图像（王聪方法）。基于过程的对称性，也同样能够证明 e = 1 。

另外，非弹性碰撞 0 \leq e < 1 。当完全非弹性碰撞时， e = 0 。

2. 非弹性碰撞损失的机械能
碰撞前后总动量守恒：m_1 v_{10} + m_2 v_{20} = m_1 v_1 + m_2 v_2
恢复系数： e = \frac{v_2 - v_1}{v_{10} - v_{20}}
联立后，可算得机械能损耗量： \Delta E_k = \frac{1}{2} \cdot \frac{m_1m_2}{m_1 + m_2} \cdot (v_{10} - v_{20})^2 \cdot (1 - e^2)

从公式可知，恢复系数 e 越小，初始相对速度越大，能量损失就越显著。如何理解这个公式？

3. 约化质量
在两个物体的力学模型中，我们可以将两个相互作用的物体的运动问题转化为一个物体相对于另一个物体的相对运动问题，从而简化计算，计算时等效的质量就是约化质量。
约化质量通常用 \mu 表示，其计算公式为： \mu = \frac{m_1m_2}{m_1 + m_2}
形式类似电阻并联形式。

碰撞过程机械能损耗量的公式中，存在这个约化质量及相对速度，可视为在相对运动视角下， \Delta E_k = \frac{1}{2} \mu v_{\text{r}}^2 (1 - e^2) 其中 e 则取决于碰撞物体的材料等。

三、柯尼希定理
柯尼希定理是质点系运动学、物理学中的一个基本定理，其文字表述是：质点系的总动能等于质心的动能，加上各质点相对于质心平动坐标系运动所具有的动能。

1.具体推导过程如下：
考虑质量分别为 m_1 和 m_2 的两个物体，其初始速度分别为 v_{10} 和 v_{20} 。
系统的质心速度为：V_c = \frac{m_1 v_{10} + m_2 v_{20}}{m_1 + m_2}
系统总动能为两物体动能之和： E_{k\text{all}} = \frac{1}{2} m_1 v_{10}^2 + \frac{1}{2} m_2 v_{20}^2
每个物体相对质心的速度为： v_1' = v_{10} - V_c, \quad v_2' = v_{20} - V_c
将原速度表达为质心速度与相对速度之和： v_{10} = V_c + v_1', \quad v_{20} = V_c + v_2'

带入动能并展开平方项，并将总动能拆分为三部分： E_{k\text{all}} = \frac{1}{2}MV_c^2 + \frac{1}{2}m_1v_1'^2 + \frac{1}{2}m_2v_2'^2 + V_c \cdot (m_1v_1' + m_2v_2')

在质心参考系中，系统总动量为零，第三部分为0.
总动能简化为： E_{k\text{all}} = \frac{1}{2}MV_c^2 + \frac{1}{2}m_1v_1'^2 + \frac{1}{2}m_2v_2'^2
柯尼希定理表明，系统的总动能等于质心动能与各质点相对质心动能之和。这一分解在分析碰撞、刚体运动等问题时非常有用。

2. 资用能

将弹性碰撞碰撞末速度公式带入柯尼希定理，相对速度一项可以化简为： E_{k\text{r}} = \frac{1}{2} \cdot \frac{m_1m_2}{m_1 + m_2} \cdot (v_{10} - v_{20})^2

可见柯尼希定理中第二项相对质心动能，为碰撞中可消耗机械能的最大值。碰撞过程中，整个系统不受外力，只有内力作用的时候，质心的动能是不变的，只有第二项可以转化，这个能量叫资用能，表示可以用来消耗的能量。如果不消耗，则为弹性碰撞，有消耗则为非弹性碰撞，同理全部消耗则为完全非弹性碰撞。

三、对传送带生热“相对动能法”的解释
如果把传送带中间过程忽略，等效为两球碰撞模型，那么，传送带速度不变，应等效为多大质量的小球？
如果质量无限大，在被碰撞后，速度不会改变。
那么系统约化质量为 \mu = m ，初始资用能为 E_0 = \frac{1}{2} \cdot m (v_{1} + v_{2})^2

初始总动能等于质心动能与资用能 E_0 之和。
根据力学原理，由于 v_2 取值不同，系统末速度也有所差异：
当 v_1 \leq v_2 时，末态资用能 E_1 = 0 。
当 v_1 > v_2 时，末态资用能 E_1 = \frac{1}{2}m(v_1 - v_2)^2 。
因此，末态总动能等于质心动能与资用能 E_1 之和。又因系统仅有内力作用，无外力介入，故质心动能在过程中保持不变。
那么，摩擦生热即为碰撞前后总动能的差值，资用能的差值，即体现为“相对动能”的差值。

思考：为什么斜传送带不能使用“相对动能法”呢？

斜传送带竖直方向有重力做冲量，故不满足动量守恒这一“相对动能法”的基本条件，所以不能使用了。

除了传送带外，还有哪些情况，可以使用柯尼希定理中的“资用能”呢？

动量守恒中的模型：如板块模型、子弹打木块、圆弧小车、冲击摆、弹簧小球等，可以秒出摩擦生热或转化的势能。

对撞机：对撞动量相反，质心动能为0，全部能量均为资用能；两个相对速度越大，资用能越大。

J的后记：在日常教学中，我时常教育学生："课堂上能听懂，只能说明老师逻辑清晰、表达准确，不代表学生领悟了知识本质，只有课后独立演算，才能真正理解因果关系，完成知识内化。"在整理这篇文章的过程中，我有了更深刻的体会。JQX首次研讨，qiusir的讲授逻辑严密，复杂过程总能抽丝剥茧简洁表述，令我茅塞顿开。但几天后在文章中复现时，才察觉那些思维过程不经由亲笔演算，很难参透这连串的逻辑链条。

“进”悟物理，“取”真求深，“芯” 火相传，“进取芯”将持续解锁知识奥秘，敬请关注！

下期预告
从动生电动势到参考系的变换——-电磁感应的另一种打开方式

一个线圈匀速进入匀强磁场的过程中，以磁场为参考系，是线圈在运动，切割磁感线，产生动生电动势；
而以线圈为参考系，是磁场在变化，于是产生感生电动势。
到底是动生还是感生？
为什么不同的参考系会给出不同的解释？
空间中的电场和磁场，真的可以相互转化吗？
下次教研，我们将围绕这个经典模型展开讨论，从两个高考题出发，一起梳理动生与感生的本质联系，走进参考系变换视角下的电磁感应。

On this day..

One Response to “动能也能“相对”······”

  1. qiusir Says:
    4月 2nd, 2025 at 16:48

    田镇旭等同学对此类问题的理解和归纳有贡献。