浜島清利:热·电磁·原子

热
T[K]=273+t[℃]
（通过PV=nRT到三个气体定律）
气体压强微观模型的推导。（这部分和台湾有的教材类似）
定压变化、定积变化、断热变化

$T(K)=273.15+t(^\circ C)$
$F_1 \frac{2L}{v_{1x}}=2mv_{1x}$，$F_1=\frac{mv_{1x}^2}{L}$，$P=\frac{F}{A}=\frac{Nm\bar{v_{x}^2}}{V}$，$P=\frac{1}{3}\rho \bar{v^2}$（气体压强后我们感受到的风力的关联因素）
$\bar{E_k}=\frac{3PV}{2N}=\frac{3nRT}{2N}=\frac{3RT}{2N_0}=\frac{3}{2}kT$（台湾教材翰林版[?]）

设边长为L的立方体内，x方向单个气体分子动量变化$2mv_x$，时间t内碰撞次数$\frac{v_xt}{2L}$，$2mv_x\times\frac{v_xt}{2L}$，$Ft=\frac{m\bar{v_{x}^2} t}{L}\times N$，$F=\frac{Nm\bar{v_{x}^2}}{3L}$，$P=\frac{F}{L^2}=\frac{Nm\bar{v_{x}^2}}{3V}$
$P=nRT=\frac{N}{N_A}RT$，$\frac{1}{2}m\bar{v^2}=\frac{3}{2}\frac{R}{N_A}T=\frac{3}{2}kT$
理想气体内能
$U=N\times\frac{1}{2}m\bar{v^2}=\frac{3}{2}nRT$
对于等压变化气体做功，$W=P\Delta V=nR\Delta T$

电磁
$k=\frac{1}{4\pi\varepsilon}$，$N=\frac{kQ}{r^2}\times 4\pi r^2=4\pi kQ=\frac{Q}{\varepsilon}$
法则（定律）$\varepsilon$诱電率诱電体的诱電率
$\frac{1}{2}mv^2+qU$=一定（类比重力势能的qV）

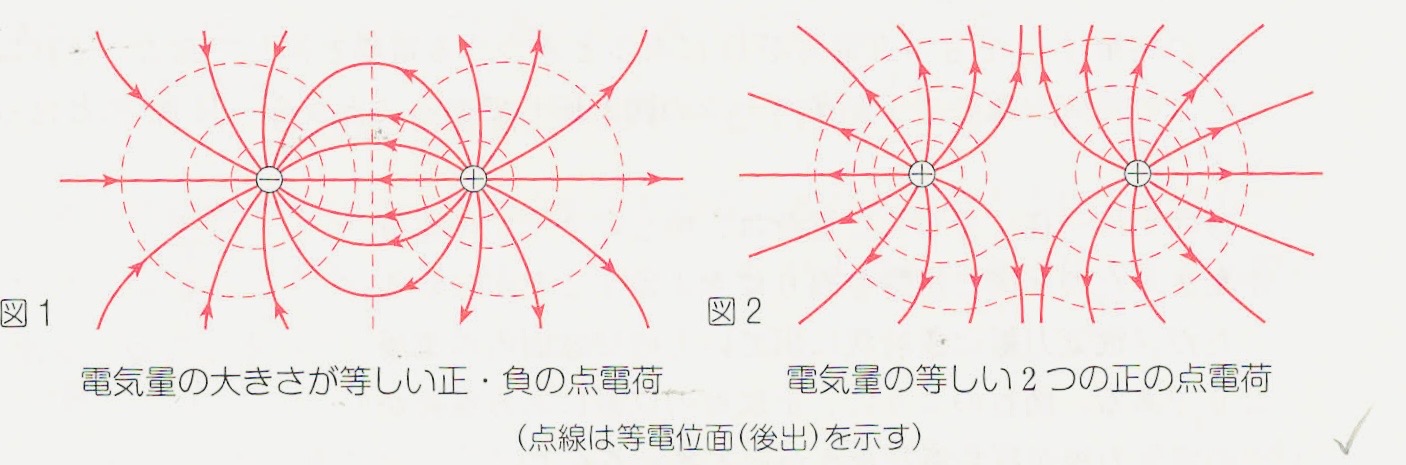
（上图和很多网图相比那是相对精确了）
点电荷的电势类比万有引力，并用高度坡度下滑类比。
等电位面（等势面）

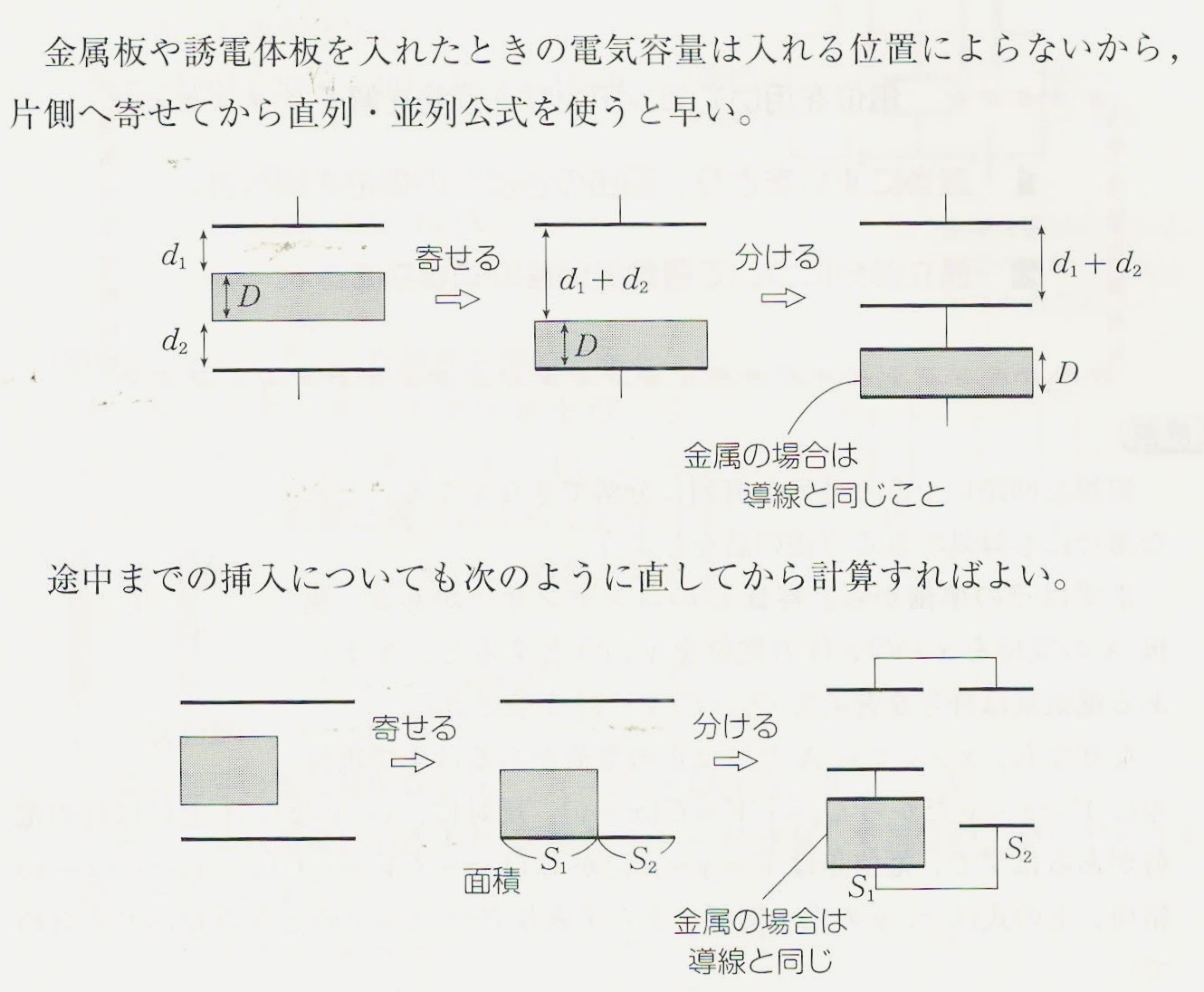
（电容器内部填入导体的等效变形很漂亮的简化）

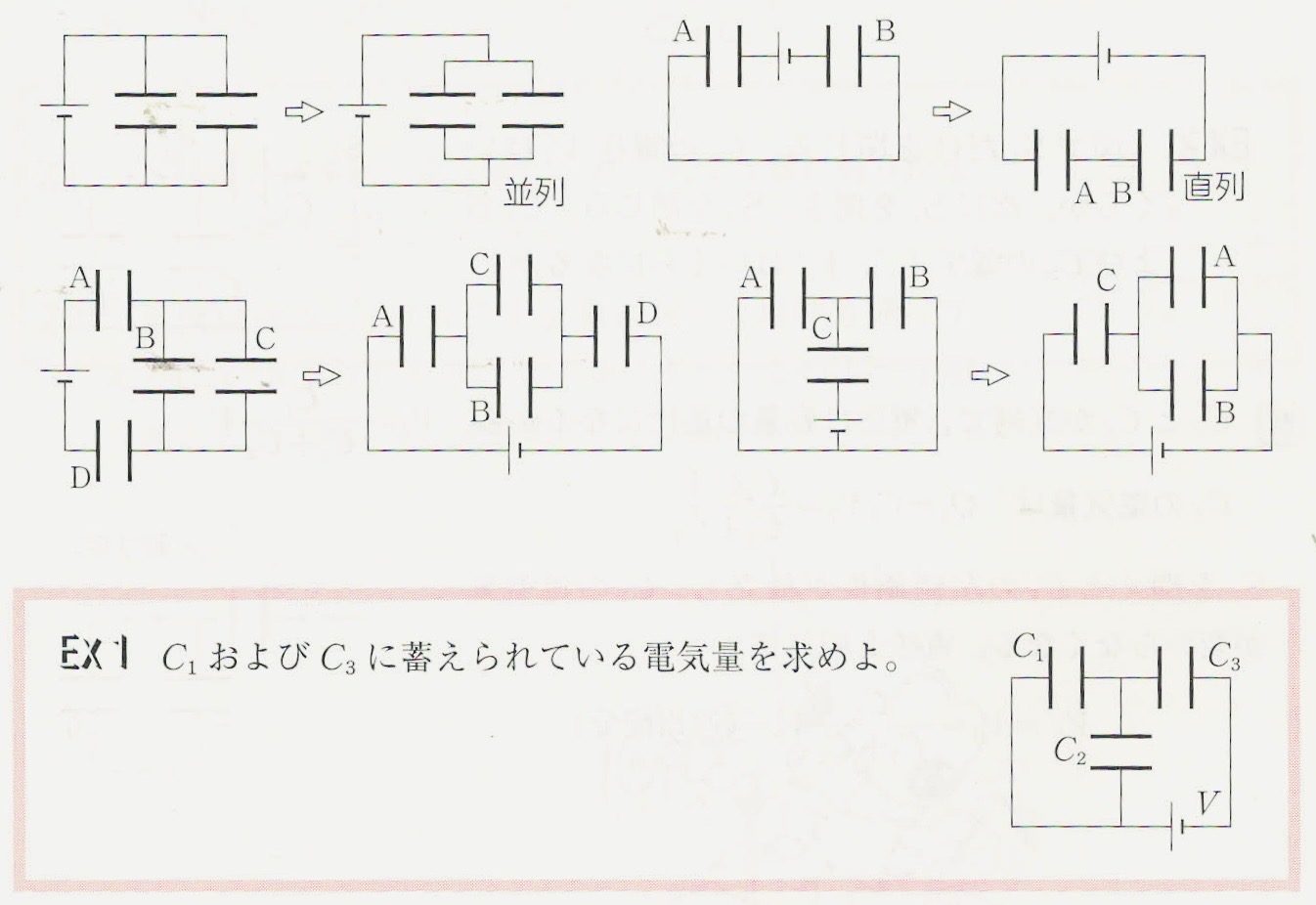
电容的串并联图和电阻的等效变换一样（图很赞）
电容储存能量的公式
平行板电容器板间吸引力
假定上极板向上平移一小段距离，从电容器能量的变化考虑$F\Delta d=\Delta U$
$\Delta U=\frac{Q^2}{2C’}-\frac{Q^2}{2C}=\frac{Q^2\Delta d}{2Cd}$
综上，$F=\frac{Q^2}{2Cd}$
电子在导线中收到抵抗力f=kv，等速运动时，kv=qE，$v=\frac{qE}{k}=\frac{qU}{kl}$，又由$I=vnqS$，$I=qnS`$
透磁率
$F=k_m\frac{m_1m_2}{r^2}$(m[Wb])
安培力F=IBl
$Z=\sqrt{R^2+(\omega L+\frac{1}{\omega C})^2}$

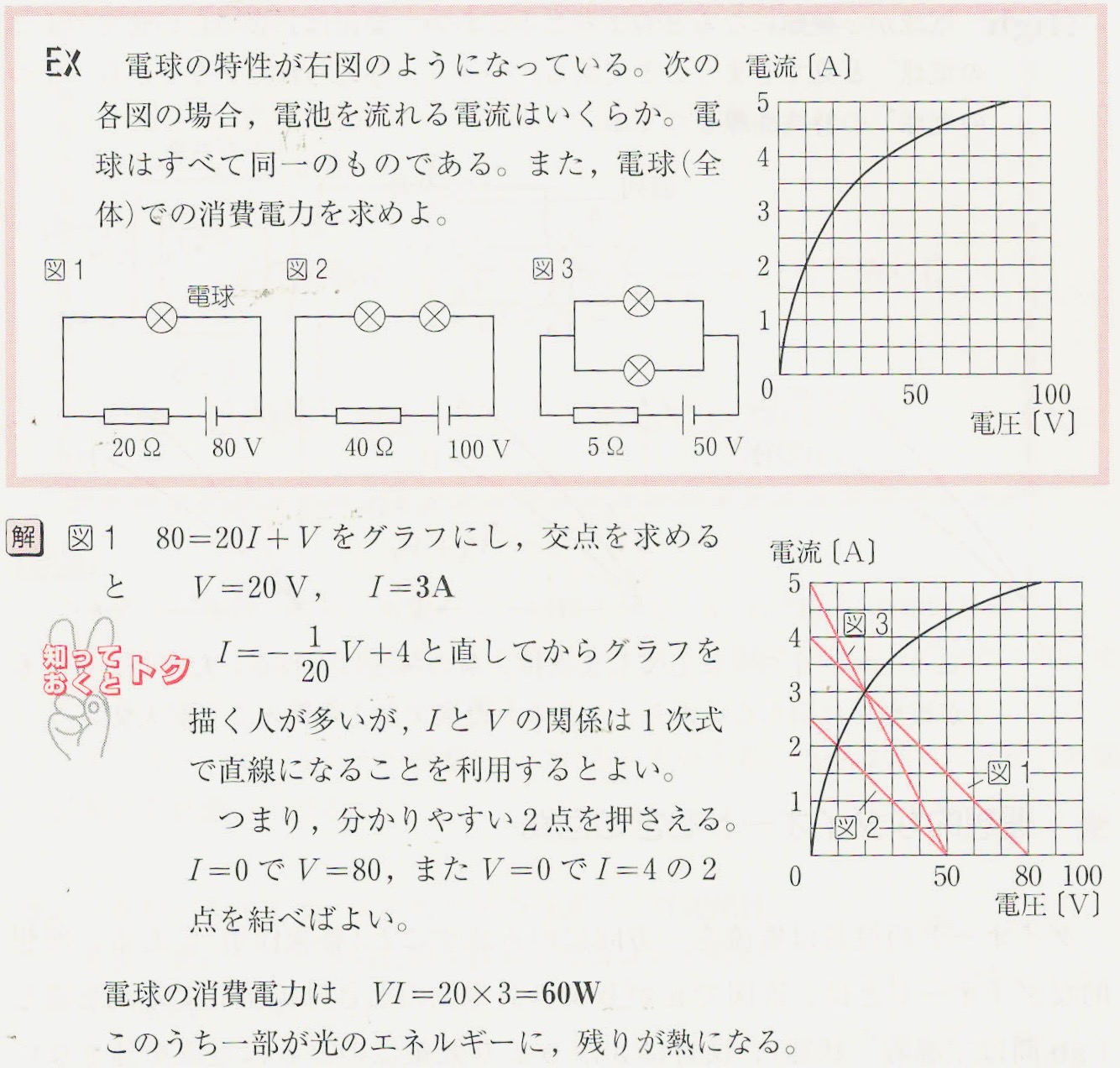
（这里一般习惯用U-I图像，通常用 $E=U+Ir$、$E=U+2Ir$、$E=2U+Ir$）
磁场诱导（电磁感应）
诱导起電力U=vBl $U=-N\frac{\Delta\Phi}{\Delta t}$
电波、赤外线、可视光线…
特殊导线的磁场

原子
光电效果、限界振动数（台阶的图示很妙）
$\frac{1}{2}mv_{max}^2=h\nu-W$
光强增大，单位时间光子数增多（同一频率）
（光子打电子，平面动量守恒的正交分解，近似求解波长变化量，赞）
光子与电子的碰撞：
$\frac{h}{\lambda}=\frac{h}{\lambda’}cos\theta+mv cos\phi$
$0=\frac{h}{\lambda’}sin\theta-mv sin\phi$

$h\frac{c}{\lambda}=h\frac{c}{\lambda’}+\frac{1}{2}mv^2$
（一系列化简和近似）$\lambda’-\lambda=\frac{h}{mc}(1-cos\theta)$

（$2dsin\theta=n\lambda$干涉条件）
（氢原子波尔模型$2\pi r=n\frac{h}{mv}$，然后推导出半径、能量与$n^2$反比）（里德常数推导）
$\frac{mv^2}{r}=\frac{ke^2}{r^2}$，$2\pi r=n\frac{h}{mv}$，$r_n=\frac{h^2}{4\pi^2kme^2}\cdot n^2$
$U=-\frac{ke^2}{r}$，$E=-\frac{ke^2}{2r}$，$E_n=-\frac{2\pi^2k^2me^4}{h^2}\cdot \frac{1}{n^2}$

（1u12gC12）$1u=\frac{12\times10^{-3}}{N_A}\times \frac{1}{12}=\frac{1}{10^3N_A}kg$
放射性崩壞、原子番号
陽子（质子）、电子、陽电子、中性子（中子）$E=mc^2$、$\Delta E=\Delta mc^2$
（经常出现保存则）
质量银行，预金+现金=一定

核分裂、核融合、γ崩壊、质量欠损
基底状态、励起状态
（这本书对于α、β和γ在磁场和电场中偏转的图示不够准确。）（β偏转比较大）
合成公式（辅助角）$asin\theta+bcos\theta=\sqrt{a^2+b^2}sin(\theta+\phi)$
二次函数的日本化简挺好
$ax^2+2b’x+c=0$，解为$x=\frac{-b’\pm\sqrt{b’^2-ac}}{a}$
三角函数公式

年终回顾
气体压强的推导过程要更熟练一点，可以转化成风的阻力问题。
$\frac{1}{2}mv^2+qU$=一定（类比重力势能的qU）

图示的辅助角公式用的很巧妙，会用就好。
小角度的近似应该加入。
$sin\theta\approx\theta$
$cos\theta\approx 1-\frac{1}{2}\theta^2$