最近在讲电场，翰铮同学分享他看学习心得，说有老师用“臭脚丫”类比电荷，臭味是看不见的那种物质...后来在日语班上课，还特地让打篮球的苏同学拖鞋，如果付出闻点味道的代价就能很好理解“field”倒也合算。
后来我觉得用榴莲代表带电物体可能更好，有人对榴莲的味道喜欢的不得了，而有人则唯恐避之不及，相当于同一点正负电荷受力相反...
尽管我本人不曾吃过榴莲，很多年前还写过关于它的心得：
@qiusir:榴莲似乎可以用来形容一种人，粗硬多刺的外表却裹着柔软丰实的心。不少人被其外表所拒，而能触及其内在的也未必受得那气味，但对敢能享食者来说却多有水果之王之美誉.
@qiusir:有的知识也如榴莲，不畏其表不惧味，能敢食之方知其美味.

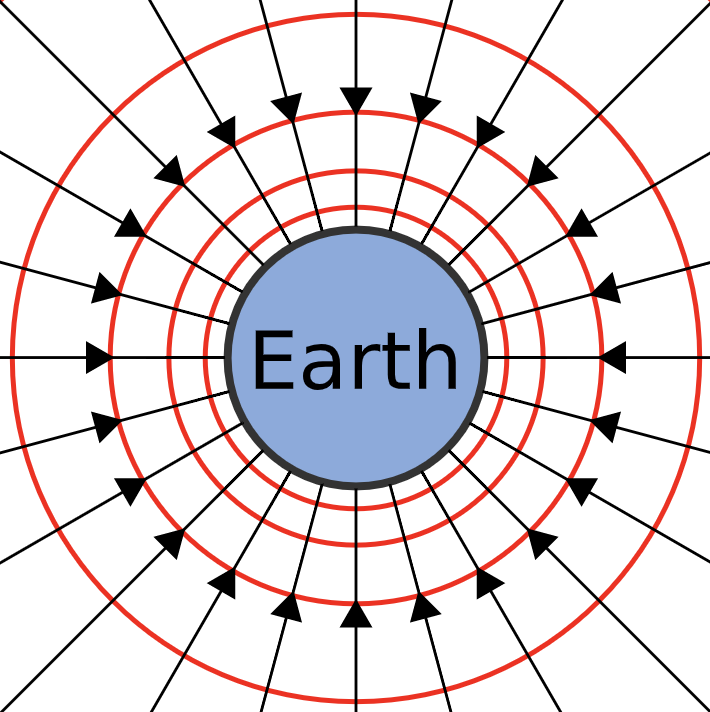
电场和引力场中的势能问题是另一个难点。在学习这件事上，也很能体现困难源自美德（深究悉讨）...
1、引力势能
$\int\frac{1}{r^2}dr=-\frac{1}{r}$
$E_p=-\int F\cdot dx$
$E_p(r)=-\int_{\infty }^{r}-\frac{GMm}{r^2}dr$
$E_p(r)=-\frac{GMm}{r}$
2、重力势能
以地面为零势面（通常是以保存力为零的位置为零势面，这里是为了表达式简洁和方便，就如通常以地面为参照物一样）
$E_p=-\frac{GMm}{h+R}-(-\frac{GMm}{R})$
$E_p=\frac{GMm}{R}-\frac{GMm}{R+h}$
$E_p=\frac{GMm}{R}(1-\frac{1}{1+\frac{h}{R} })$
如果物体在地球表面附近，h$\ll$R，$\frac{1}{1+\frac{h}{R} } \approx 1-\frac{h}{R}$
$E_p\approx\frac{GMm}{R^2}h$
所以有$E_p\approx mgh$，也就是有心力场局部近似为匀强的引力场。
3、电势能
类比万有引力$F=\frac{GMm}{r^2}$和库仑定律$F=\frac{kQq}{r^2}$
不难得出对于异种电荷间的电势能和引力势能具有相同表达式，$E_p(r)=-\frac{kQq}{r}$（此处Q,q仅指电量大小）
如果考虑到电荷的正负问题，以及r的方向问题，库仑定律更一般表达$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over F} = k \frac{{Qq}}{{{r^2}}} \hat{r}$，Qq是包含电性正负的...（$\mathord{ \buildrel{ \lower3pt \hbox{$ \scriptscriptstyle \rightharpoonup$}} \over F} =-G \frac{{Mm}}{{{r^2}}} \hat{r}$）


电势能的表达式：$E_p(r)=\frac{kQq}{r}$
由电势的定义式$\varphi =\frac{E_p}{q}$，也就方便得出点电荷的电势决定式：$\varphi =\frac{kQ}{r}$
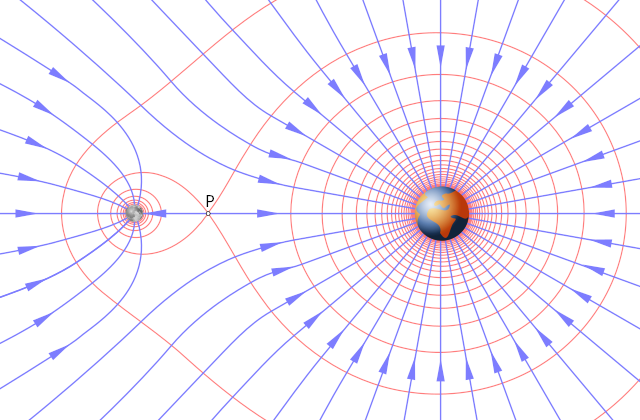
如此容易理解，正电荷的电场电势为正，负电荷的电场电势小于零；负电荷在负电荷电场的电势能大于零...对等量异种电荷中垂线为零势能面，除了用电场力方向理解，用$\varphi =\frac{kQ}{r}+\frac{-kQ}{r}=0$理解更直接...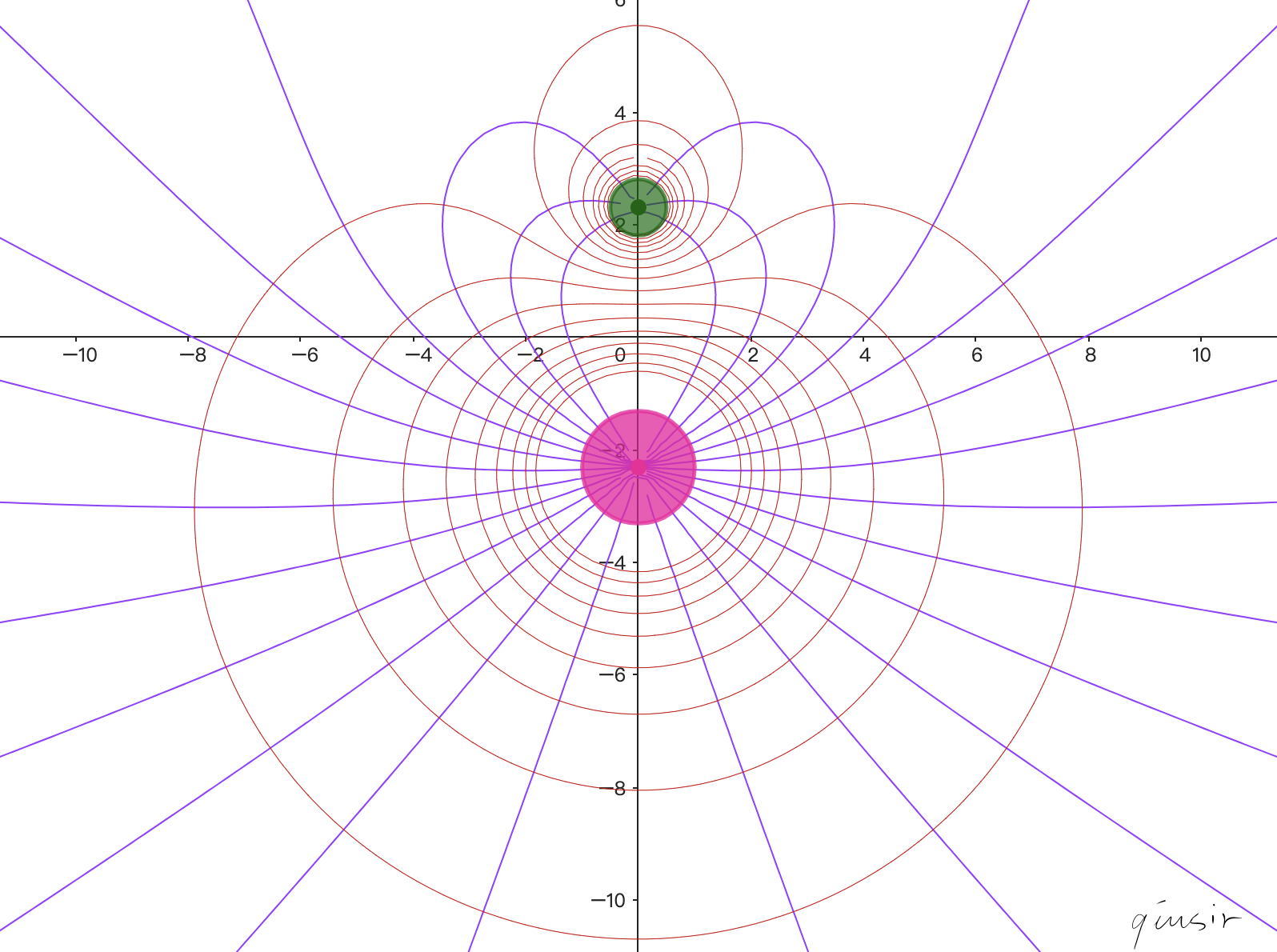

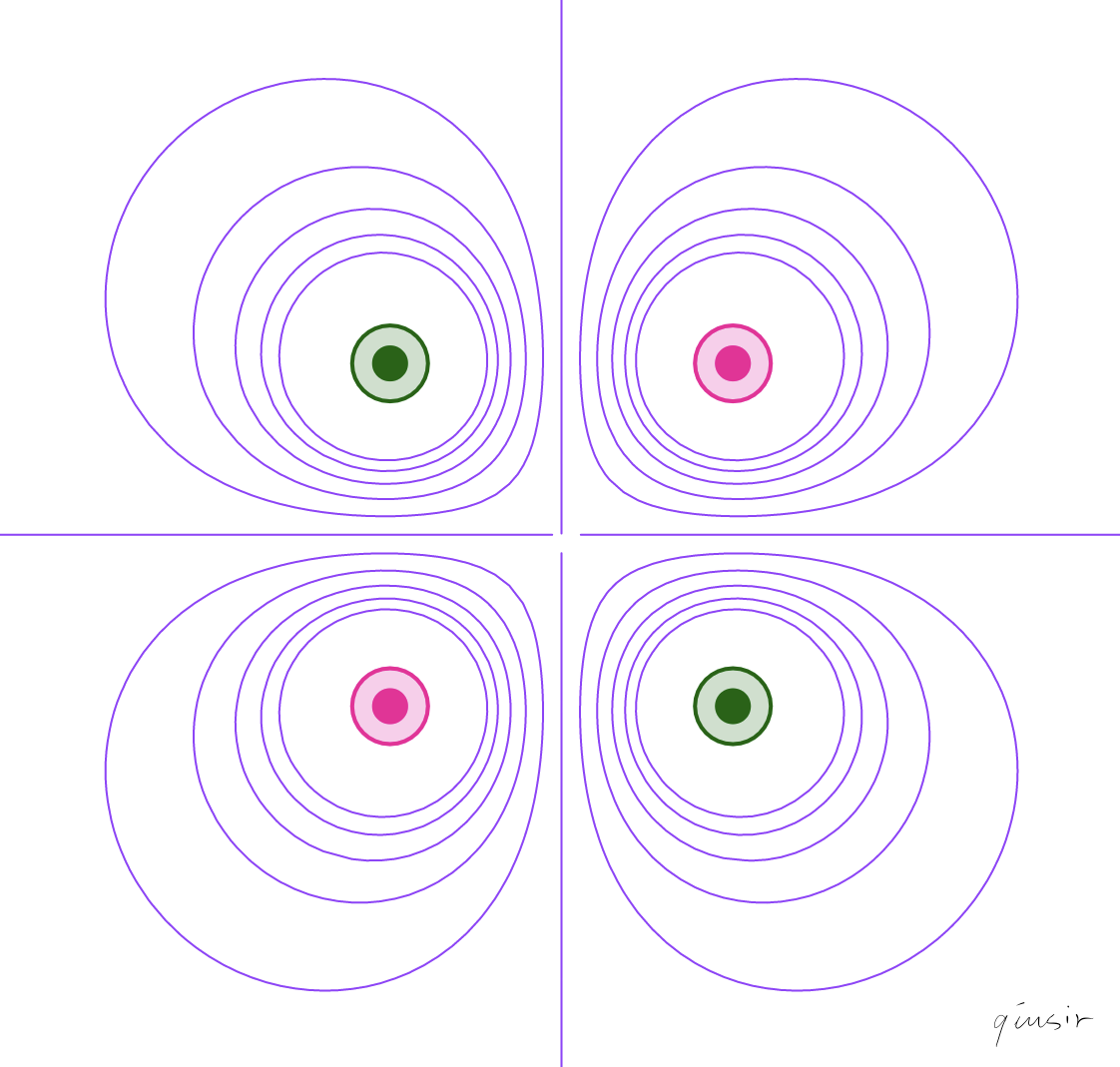
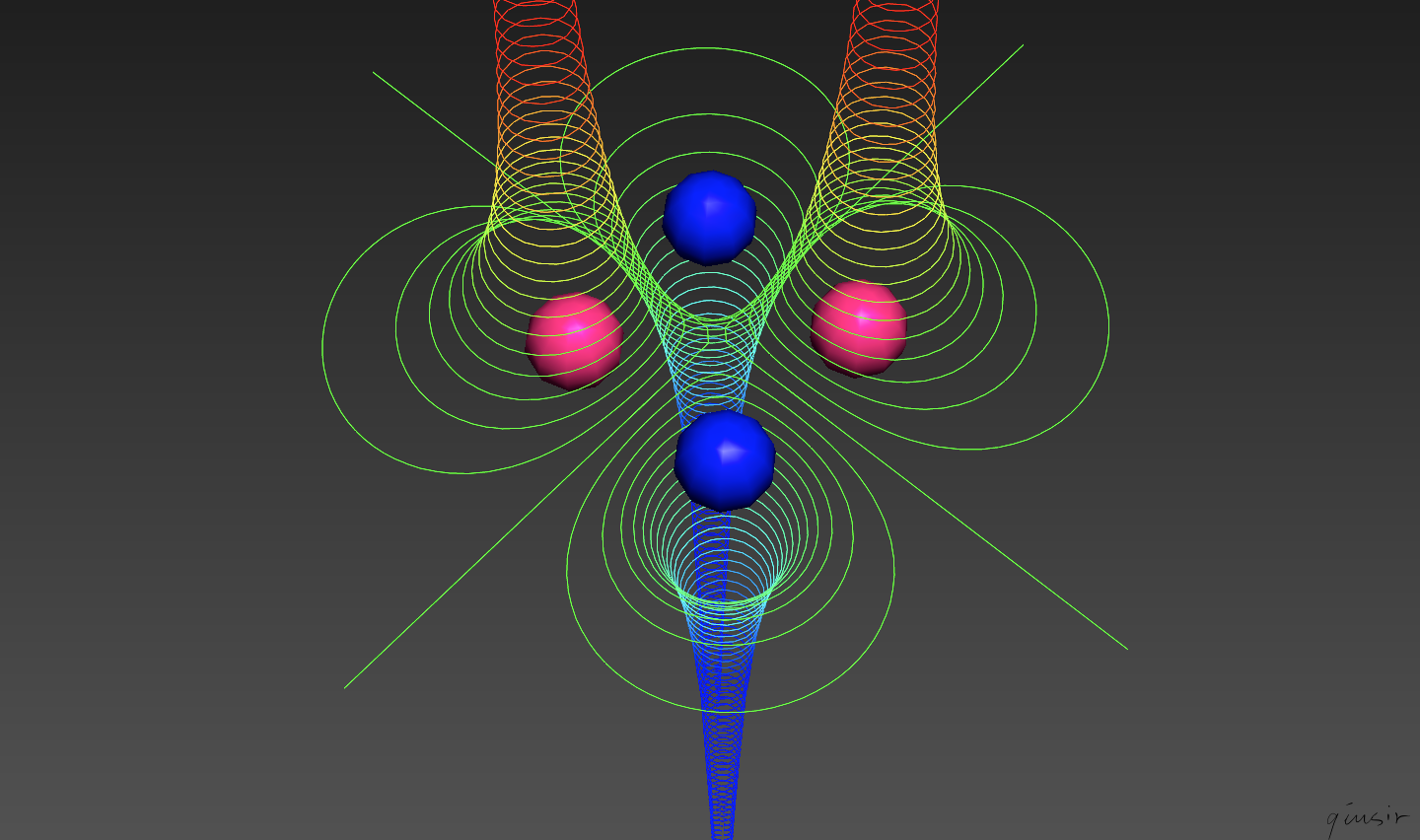
套用点电荷电势的方程，可以得出关于两个关于y轴对称的点电荷在平面某点的电势：
$\varphi_n=\frac{k_0Q_1}{\sqrt{(x+l)^2+y^2}}+\frac{k_0Q_2}{\sqrt{(x-l)^2+y^2}}$
电场是保守力场...电场线方程和等势面方程互为共轭调和函数（不懂，安排远卓等同学暴力求解去了）...
$\psi_n=\frac{k_0Q_1(x+l)}{\sqrt{(x+l)^2+y^2}}+\frac{k_0Q_2(x-l)}{\sqrt{(x-l)^2+y^2}}$
根据上年的两个方程，用GeoGebra的曲线“序列”就可以绘制上图了...
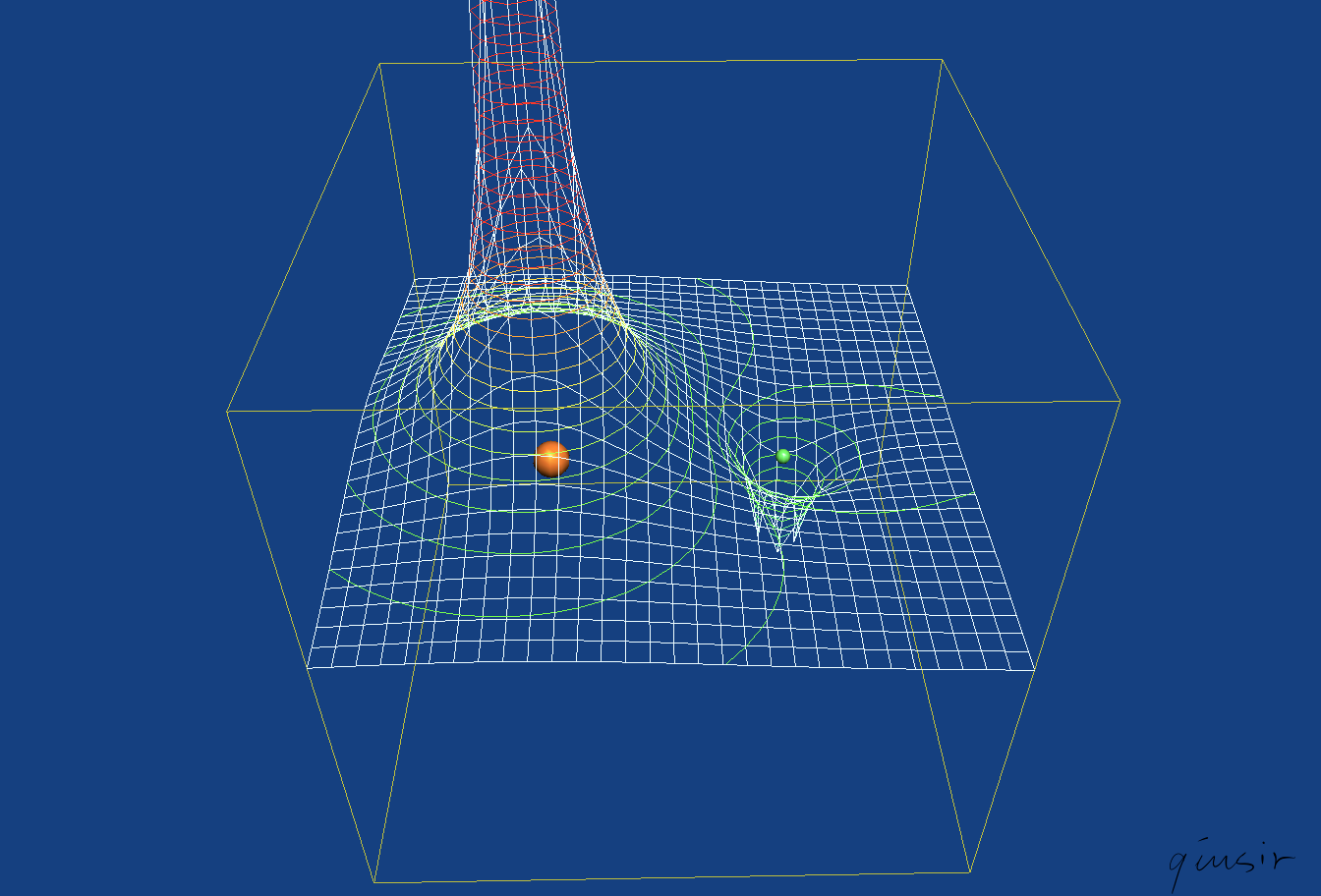
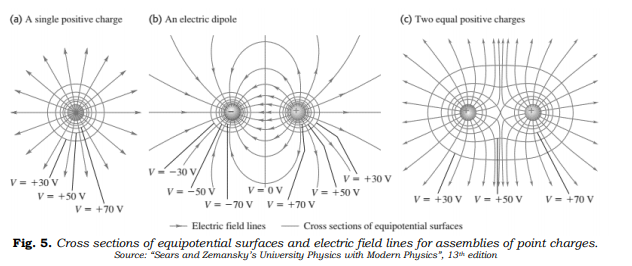
另，最近这里[?]发现这张图，按照这里物理量表达习惯略微做了修改（日本教材中，U代表势能，而电势用V表示）：

关于电势的高低，用地势的高低类比，而等势面和地里的等高线类同...

On this day..

• what if - 2019
• 莫避春阴上马迟,石干 - 2016
• 黑板:物理公式的头脑风暴 - 2011
• 人的正负属性 - 2007
• 反正我是想您了！ - 2006
• 赤峰很近！ - 2005
• 人认知的平等性 - 2004