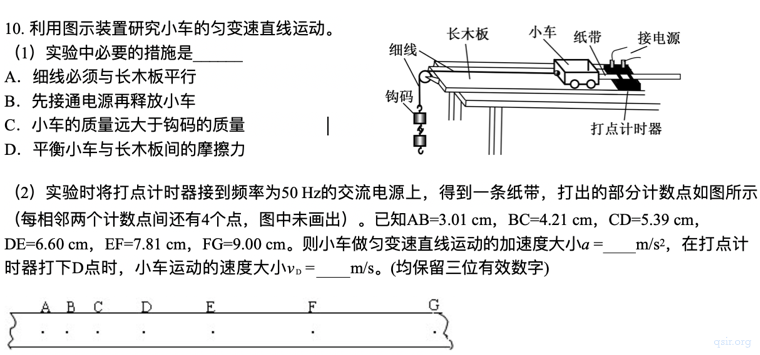
关于运动学的计算，在尝试后面的题目之前，应该先动手算完上面的这道题目[0]，审题、数据计算是摆在物理知识运用之前的两道坎。参考答案可在本文最后面找到。

这里主要推荐一道运动学计算题目的几种方法，通过具体题目分析帮助复习匀变速直线运动相关的公式。相比最基本甚至最繁琐的过程，那些有些貌似巧妙的方法不过是“雕虫小技”，技巧是有前提的，作为学生更应该重视基本方法，先完成繁杂的计算，那会带给你信心，然后才有可能发挥你物理方面的才智，才会有创意的火花迸发...

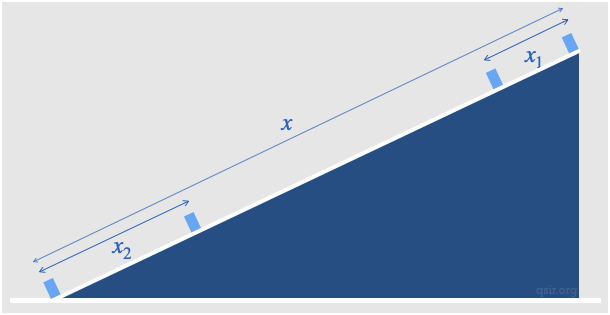
[1]一物体（不计大小）由静止从斜面顶端下滑到斜面底端，最开始的一段时间下滑了$x_1$，最后一段相同时间下滑了$x_2$，求斜面的总长度$x$。
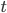设物块从斜面上匀加速下滑的加速度为$a$，运行总时间为$t$，运行到斜面底端的速度为$v_t$，前后两端相同的时间为$T$。
最开始的一段时间内：$x_1=\frac{1}{2}aT^2$（后面有的方法用到就略去此方程了）方法一：
$x_2=a(t-T)T+\frac{1}{2}aT^2$
$x=\frac{1}{2}at^2$
通过计算可得：$x=\frac{(x_1+x_2)^2}{4x_1}$
这种方法最可贵的就是让自己有耐力突破貌似繁杂的计算屏障，这是不应该省去的过程...
方法二：
相比位移的基本公式$x=v_0t+\frac{1}{2}at^2$，利用运动可逆还是$x=v_tt-\frac{1}{2}at^2$
由$x_2=v_tT-\frac{1}{2}aT^2$得$v_t=\frac{x_1+x_2}{T}$
再由$2ax=v_t^2$即可得上述结果。
兼具第一种方法的过程清晰的优点，同时计算量要少很多。
方法三：
利用匀变速运动平均速度等于中间时刻的瞬时速度的二级结论。

$v_t=2v_\frac{t}{2}$，$v_\frac{t}{2}=\frac{\frac{x_1}{T}+\frac{x_2}{T}}{2}$
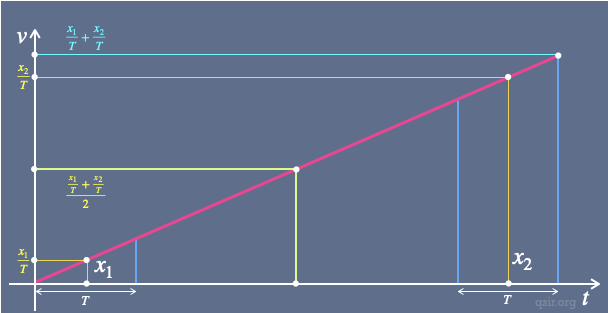
然后根据方法二的计算即可得结果。
方法四：
$(\frac{x_2}{T})^2-(\frac{x_1}{T})^2=2ax'$，$x=x'+\frac{x_1+x_2}{2}$
方法五：
$(\frac{x_2}{T})^2=2ax''$，$x=x''+\frac{x_1+x_2}{2}-\frac{x_1}{4}$
方法六：
$x_1=\frac{1}{2}at^2$ $x_k=\frac{1}{2}a(kt)^2-\frac{1}{2}a((k-1)t)^2$
$\frac{x_k}{x_1}=2k-1$（这里的k只需大于1未必是整数）由此可得
$\frac{x_2}{x_n}=2k-1$得出$k=\frac{x_1+x_2}{2x_1}$
由$x=k^2x_1$可得前面结果。
方法七：
参照前面k未必是整数的方法，可以根据$x_n-x_m=(n-m)aT^2$变形得$x_k-x_1=(k-1)aT^2$
由此，$x_2-x_1=(k-1)aT^2$由前面$x_1=\frac{1}{2}aT^2$同样可得出$k=\frac{x_1+x_2}{2x_1}$
然后同方法六。
方法八：

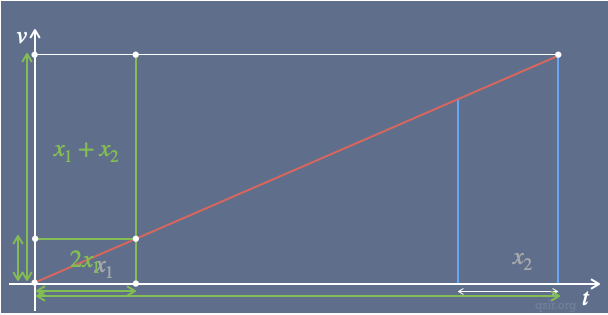
这些方法中，最简单的算是直接构造图形面积来求得了。
根据上图面积可求得$\frac{t}{T}=\frac{x_1+x_2}{2x_1}$，又$\frac{x}{x_1}=(\frac{t}{T})^2$
由此可得$x=\frac{(x_1+x_2)^2}{4x_1}$
P.S.
张士博同学（分流成绩第一那位）用到了一种相对特别的方法。
利用a-x图像，$v_1^2=2aL_1$,$v_1=\sqrt{2aL_1}$,$v^2=2aL$,$v^2-(v-\sqrt{2aL_1})^2=2aL_2$...
相关题目[2]推荐：

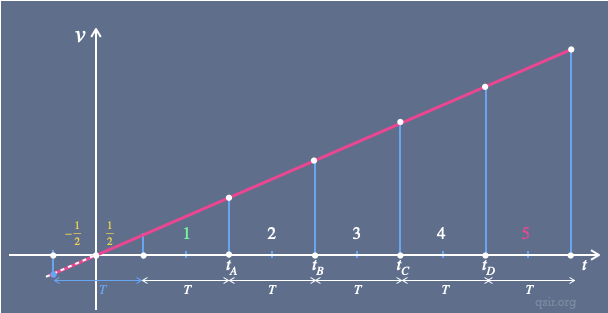
物体自O点由静止开始做匀加速直线运动，依次经过运行轨道上的A、B、C、D四个点，测得AB=2m,BC=3m，CD=4m，且通过AB、BC和CD所用时间相同，求OA的距离。
这道题目的基本方法：可设定到A的时间为t，其他时间间隔T，$x=\frac{1}{2}at^2$,$\overline{AB}=atT+\frac{1}{2}aT^2$，$\Delta x=aT^2$
很多人也想到了面积比例的方法，关联后面的这道题目。
记得不少学生Shocked by 我把初速度为零拓展到反向加速（整个过程加速度不变）的方法，相同时间的位移从2、3、4外推到5、6、7，而往回推是1，然后是0，对，所以出发点必然是$\frac{T}{2}$...
答案：$\frac{9}{8}$
这种题目还可以拓展到平抛运动[3]。图中为边长为10厘米的正方形网格。O、A、B和C为某平抛运动上的四个点，相对位置如图。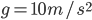$g=10m/s^2$，求$v_A$

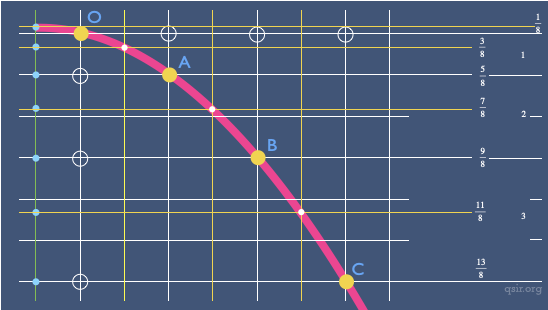
对于匀变速运动相同时间内通过的位移比是1：2：3的特殊情况，我们可以从数字组合的角度转换为更为习惯的1：3：5
$1=\frac{3}{8}+\frac{5}{8}$，$2=\frac{7}{8}+\frac{9}{8}$，$3=\frac{11}{8}+\frac{13}{8}$，而最开始的运动时间是$\frac{T}{2}$，对应的位移为$\frac{T}{8}$...
P.S.张子义同学构造平行线构造出初速度为0然后利用13579的方法很巧妙...

[4]去年全国II的答题里，涉及到的数据是$x_1=24m$，$x_4=1m$，同上面的分解一样，24=13+11，接下来应该是[9,7],[5,3]，最后的第4秒里只要0.5秒运动，位移为1，倒过来就是[0、1]、[3、5]、[7、9]、[11、13]...
答案：$\frac{5}{2}m/s$
最朴素的一般方法才是正道，这里推荐多种方法的目的除了是检验基本概念的理解和运算之外，才是创意的分享，但一定要知道大多算是雕虫小技。另外一道曾经的高考题也适合放到这部分练习一下：
[5]一物体由静止开始以加速度$a_1$匀加速运动了一段时间，加速度突变为$a_2$又经过相同的时间物体恰回到了出发点，求$\frac{a_1}{a_2}$
有时间的话会详细整理一下几种常见的方法。
1、位移为零的标准方法:$\frac{1}{2}aT^2+a_1TT+\frac{1}{2}a_2T^1=0$
2、速度为零的时间t:$\frac{1}{2}a_1T^2+\frac{1}{2}a_2t^2=\frac{1}{2}a_2(T-t)^2$,$a_1T=a_2t$
3、平均速度:$\frac{a_1T}{2}=-\frac{a_1T+a_1T+a_2T}{2}$
4、速度时间图像面积:
5、王上同学设定前后两端时间没的位移和利用平均速度等于中间时刻瞬时速度的方法很巧妙:$v_{\frac{T}{2}}=\frac{x}{T}$,$v_{2T}+2\frac{x}{T}=2\frac{-x}{T}$,$a_1T=2\frac{x}{t}$,$a_2T=-\frac{4x}{T}-\frac{2x}{T}$...
6、张博涵的图像割补法，有学生称之为飞镖的割补法也很通用...
答案$\frac{1}{-3}$，可自行把第二段时间换成2T后如果用两种以上方法算出同一个答案算是过关，如果没有一遍过，可以继续3T...
第零题答案：AB 1.20 0.600

P.S.俊达问了道题目，他好奇有没有“帅”的方法
“匀加速运动的物体，从A到B速度增加了v，位移为$x_1$，从B到D速度增加了2v，位移为$x_2$，C为BD中间时刻经过的点，求BC的位移$x$”
方法1:用平均速度 $\frac{x_2}{2T}=\frac{x_1}{T}=a\frac{3}{2}T$...
方法2:用相邻相同时间间隔内位移相等 $x-x_1=x_2-x-x$
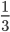方法3:刘书傲等同学用了速度时间图像的割补法，觉得很赞。构造以整个过程中间时刻速度为高的矩形，面积$x_1+x_2$，而BC的位移$x$是以中间时刻速度为高宽为总时间$\frac{1}{3}$的矩形面积，占总面积的$\frac{1}{3}$...
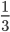方法4:李欣然同学对上面方法的解释，联系前面的题目，提出整个过程的平均速度和BC段（关于中间时刻对称）的平均速度相等，而时间是总时间的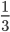$\frac{1}{3}$...
答案：$\frac{x_1+x_2}{3}$
Update202103

一道题目的开放解法，所用到的公式基本上涵盖了匀变速运动，而十多种方法的讨论也只能是师生有效的协作才能完成，几位同学贡献了很好的思路。
Update202302

·可能有点用的物理学习资料[?]

On this day..

• 今朝放鹤且冲天 - 2024
• 我的世界观 - 2023
• 手拿板砖的警察很有爱 - 2022
• 文字的时光隧道 - 2005
• 勇气\度量\智慧 - 2004
• 什么是教育中的守恒？ - 2004