七 24

等时圆与最速轨道

教研|〖数理探究〗, 高三|〖苦海泛舟〗 qiusir 2010

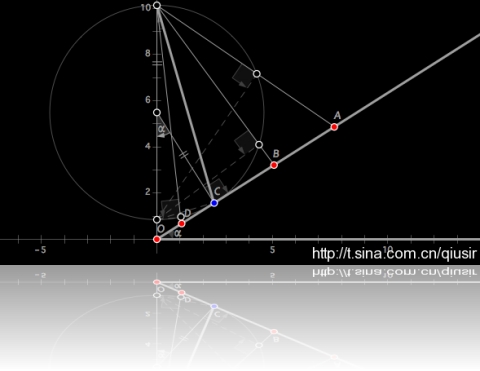
等时圆：滑快从两端搭在竖直放置的圆上的光滑轨道无初速度下滑，且轨道至少一端过竖直方向直径上的一个端点，则下滑的时间相同。因为和圆相关，这里姑且叫做等时圆问题。这个结论很有趣，证明起来也很简单。

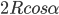设圆半径为R，轨道与竖直方向夹角为\alpha，则轨道长度为2Rcos\alpha，滑快下滑的加速度为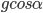gcos\alpha，下滑时间为t，所以有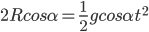2Rcos\alpha=\frac{1}{2}gcos\alpha t^{2}，可以看到下滑时间与角度\alpha无关，都等于从竖直直径的自由落体的时间。

dtc.jpg

由上面的结论一样可以设计出很有趣的题目，比如最速轨道的选择问题。说从某点P为起点到倾角\alpha的斜面上搭起的光滑轨道中，滑快在哪一条轨道上下滑的最快呢？首先以点P为直径上的一个端点，在竖直方向绘制圆，利用上面的结论，在同一圆上的轨道下滑时间相等，那最短的无非是对应圆的半径最短的了，也就是和斜面相切的那圆对应的轨道。

上图中已经给出很精细的构造，利用几何关系能够知道，与竖直方向夹角为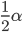\frac{1}{2}\alpha的那条就是最速轨道了。

On this day..

2 Responses to “等时圆与最速轨道”

  1. qiusir Says:
    12月 22nd, 2011 at 15:23

    如果考虑摩擦？龙宣宇的等效重力是很好的方法

  2. 转“捻”之间|求师得20年 Says:
    5月 24th, 2013 at 15:44

    [...] 以后也有过很多PWW(Proof Without Words)范例，比如梯子模型（等棍问题，XY轴上到定点距离平方和为常数[?]与然轴上到定点距离和是常数有很大不同[?]）
、质点几何学、等时圆[?]等，都是通过开放通道引发很多知识的再创造的典型范例...

 在选择MIT CSAIL前，成禹已经获得了数学和信息学两个学科领域的奥林匹克竞赛五块奖牌（2G+2S+1B）[?]，“中点多边形”是他还在初中学段时在我数理选修课上利用构造线段和中点的快捷键“捣乱”的发现。 [...]