四 14
该守规矩的时候总有人只图自己方便,不该守规矩的地方,却成了百般乖巧的良民了。教学大纲大概就是这么个类似无形绳索的东西。既然积分/变化率和导数/微元累积的思想早在物理上体现,积分和导数的工具是不是也该在中学的物理中松松绑了呢?
一般来说,简谐振动可以从运动的特殊性为线索引入。比如一般的运动分类,机械运动、热运动、电磁运动...有同学还说社会运动:)而就机械运动来说,静止、匀速直线运动、匀变速直线运动、匀变速曲线运动、匀速率圆周运动...(接下来特殊点的会是什么样的运动呢?)
从受力的角度看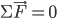 对应的平衡态,
对应的平衡态,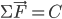 对应的匀变速运动(直线和曲线),
对应的匀变速运动(直线和曲线),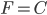 对应的匀速率圆周运动...接下来的运动一定是“非匀变速直线运动”了,而从受力的角度更容易想到特殊的受力情况,
对应的匀速率圆周运动...接下来的运动一定是“非匀变速直线运动”了,而从受力的角度更容易想到特殊的受力情况,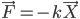 ,当然也可以让学生思考一下
,当然也可以让学生思考一下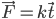 的运动情况。
的运动情况。
弹簧振子的简谐振动可以通过匀速圆周运动在直径上的投影来分析。设定圆周半径为
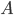 ,角速度为
,角速度为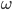 ,初相为
,初相为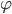 ,经过时间
,经过时间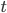 转过的角度为
转过的角度为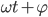 。
。旋转直径在水平方向的分量(振子位移)
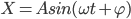
圆周运动线速度在水平方向的速度分量
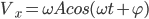
圆周运动向心力加速度在水平方向的分量
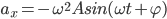
这些都符合简谐振动的特征。当然圆周运动在水平方向的投影时简谐振动,也可以从回复力的角度证明。向心力在水平方向的分力
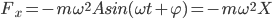
通过简谐振动的位移时间图像
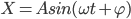 ,利用导数可以得出速度、加速度的时间关系图像(当然反过来考虑积分的问题也未尝不可)。即便不用导数,单从速度是位移的变化率、加速度是速度的变化率的定义也可以接受。动态过程的想象,特殊点的分析。
,利用导数可以得出速度、加速度的时间关系图像(当然反过来考虑积分的问题也未尝不可)。即便不用导数,单从速度是位移的变化率、加速度是速度的变化率的定义也可以接受。动态过程的想象,特殊点的分析。
数学的工具在物理上恰当的应用范例会得到正向的反馈。提到正弦函数的导数问题,电磁感应的正弦交流电部分大体类似。
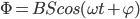
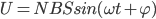 ...
...
On this day..
- MAKING LEARNING WHOLE - 2017
- 这一刻重生~ - 2014
- 最美的风景 - 2008
- ...传觉士、觉堂 - 2005
- 老师,领导,长辈也是朋友 - 2004