关于不同轨道对应速度的几何构造，花了我大半个上午的时间（有趣的问题就像时间黑洞），结果还算漂亮，不过还有一点疏忽...

很多年前（大概1997年初），曾用几何画板尝试各种方法构造过圆锥曲线，也着迷圆锥曲线的统一性，那时的软件直接实现截圆锥还非常困难（现在GeoGebra很便捷实现）。其中比较喜欢的一种构造方法是利用点到圆上半自由点连线中垂线与过该点直径（半径、直线，过圆心的射线更物理一点）交点的轨迹（这种方法构造的圆锥曲线2a是等于大圆半径的一族，这个以引力为中心半径为2a的圆应该有个酷的名字吧（这个圆应该是可以构造统一引力中心下能量为其2倍（半径为一半的圆轨道）的所有可能轨道？），对应能量是不变的前提$E=-\frac{GMm}{2a}$）...很久以来也只停留在焦点、切线和其中光学性质等层面，没想到这个模型里还包含物体在有心力场中运动速度的几何对应，很是巧妙，堪称神奇...

卫星绕地球做椭圆轨道的运动，也如地球绕太阳的运动，和单个场源电荷作用下电荷的运动，都是经典物理里的有心力场。印象中大学曾推到过运动轨迹的方程，甚至很多年后让新毕业的老师也推到过，而教师的认知很符合用进废退，也是基础教育对知识的切入点的要求，一直以来繁杂的数学表达影响了思考。
Geogebra里直接提供了“密切圆”的函数，只需要用到高中的基础知识，可以利用引力的法向分力提供向心力$F_n=\frac{mv^2}{r}$），从密切圆半径和法向力来反推速度，这样就可以绕开繁杂恐怖的数学表达了。当然也回避动态的模拟（抛物线很方便，椭圆轨道可以近似实现，双曲线不那么容易...另外在前面提到的基础构造中，椭圆的引力中心和双曲线的引力中心对应点反着...），专心去探究一下轨道上各个位置速度和对应几何上的隐藏关系...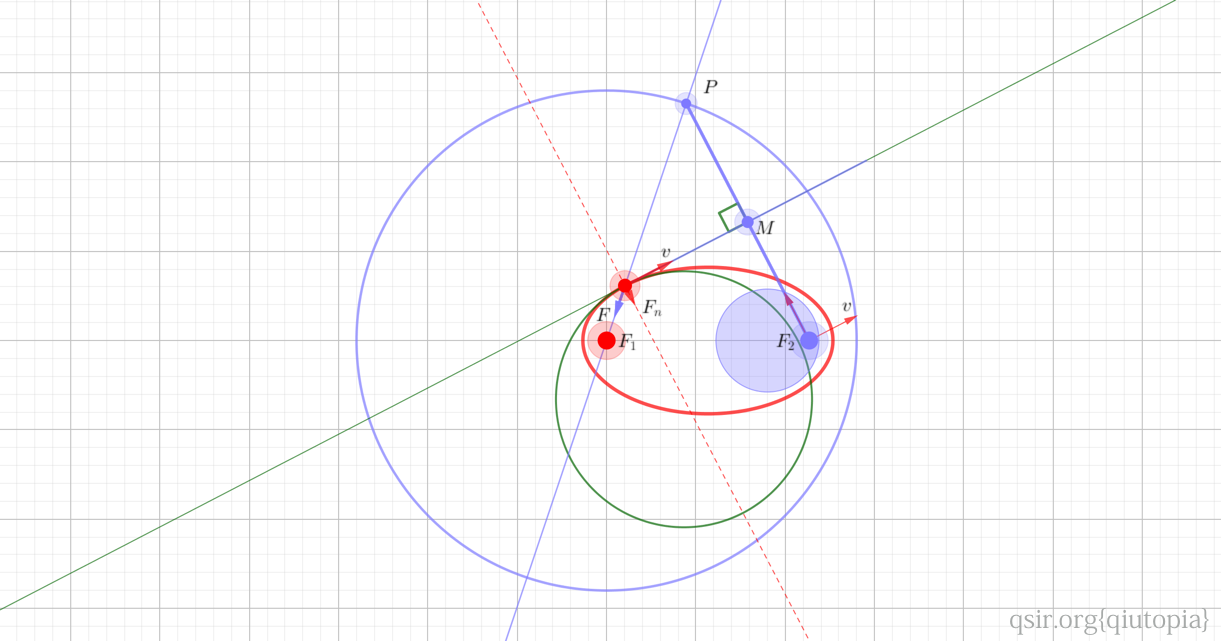

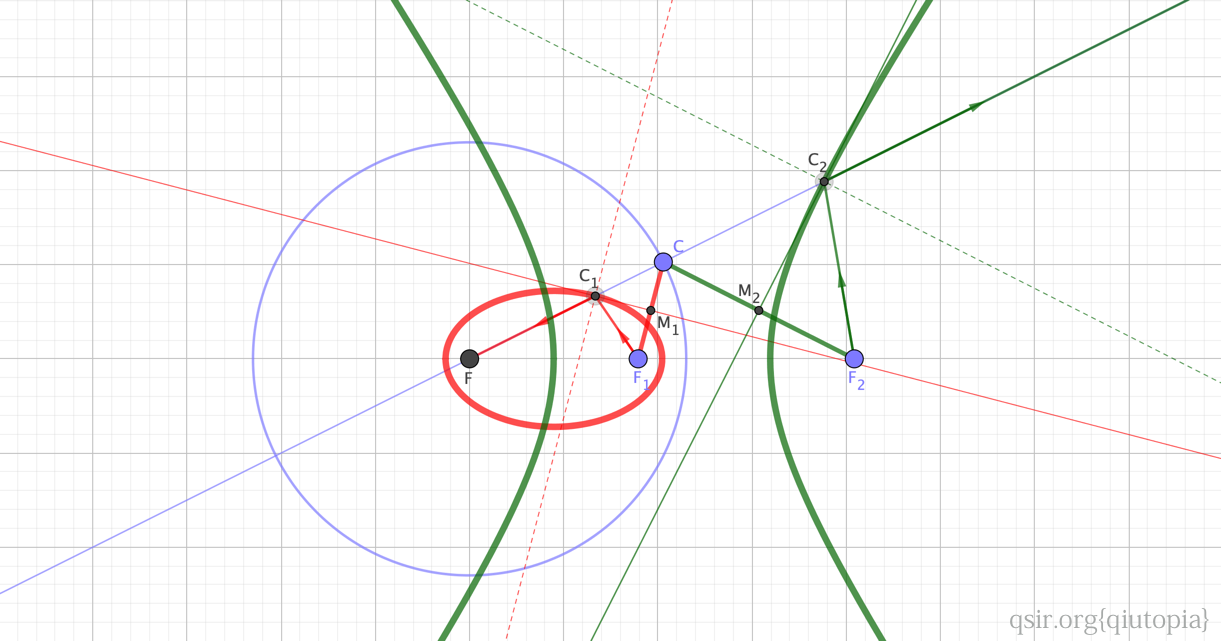
另一个焦点（非引力中心）与圆上动点连线，绕其中点旋转90°（其实就是中垂线）是圆锥曲线的切线，但这里不用直线，主要是从图形上类速度向量的平移图形。而更奇妙的是，除了速度向量平移后共圆，如果是双曲运动，速度应该也会共圆吧...

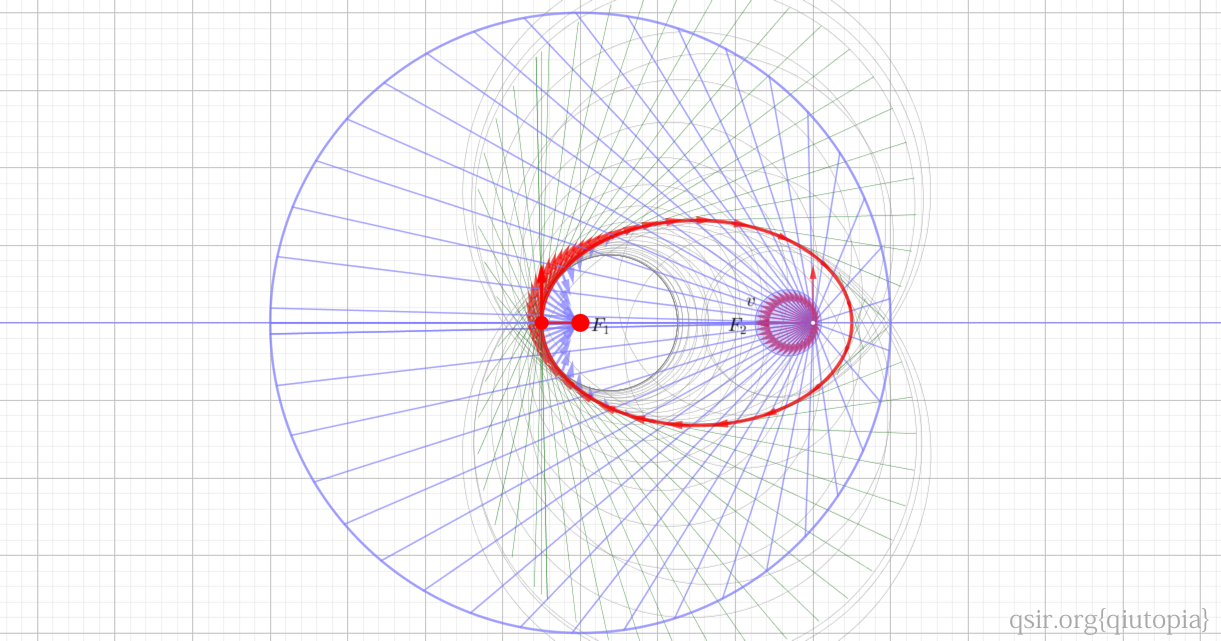
如法炮制，结论很完美，连线的绕中点的垂线段不仅是和圆锥曲线相切，而且和速度向量某种相似。不仅是速度向量平移后共圆这一点，而且发现椭圆轨道上的速度与引力中心和圆连线的长度成正比，双曲轨道的成反比。

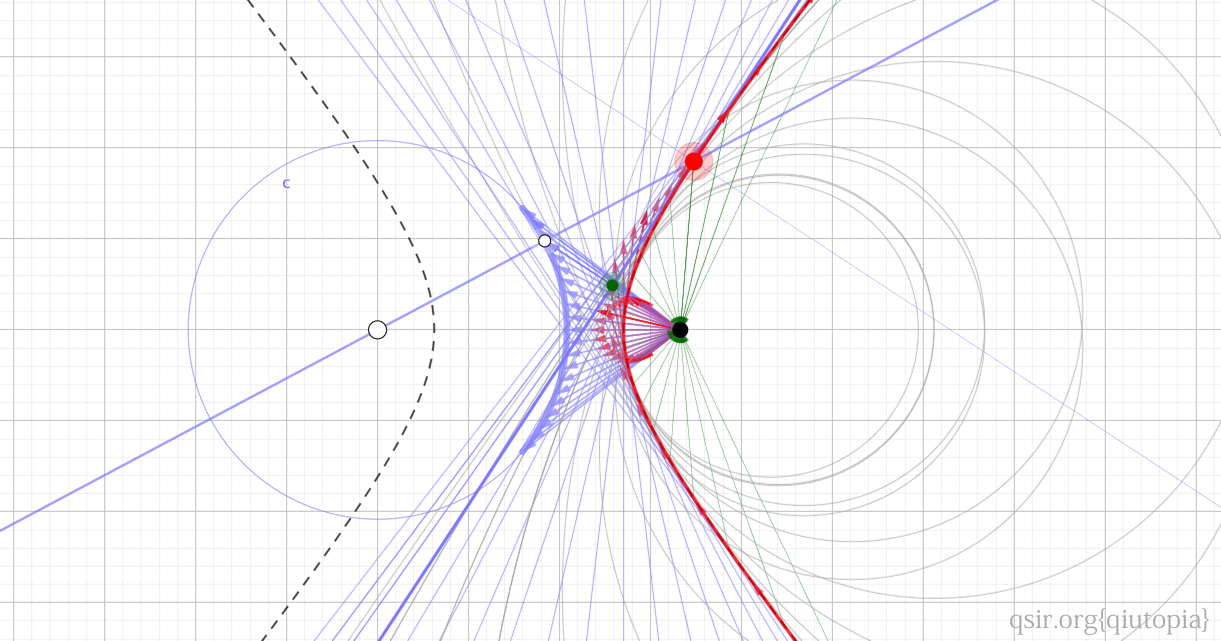
有心力场中，椭圆和双曲线的轨道已经很好的统一了，而切割圆锥能得到的圆锥曲线中还有抛物线呢，
当然从运动速度上看，类抛体运动当属最为基础的，在匀强力场中，速度变化量必然和力同向，自然速度平移后在一条直线了，但结合前面的探索，应该有另外的视角。

抛物线构造的一种方法是利用到顶点与定直线距离相等，一方面可以看成是前面构造椭圆和双曲线中圆的半径为无穷大，圆退化成直线，圆心在无穷远；另一方面，焦点到定直线（准线）的连线不仅和速度向量平移相关（一如前面椭圆和双曲线，发线方向和速度方向垂直），大小也应该也有比例关系，对，也是成正比。
倒叙，从线段长度来倒推和速度，从运动分解角度重新构造抛物线...

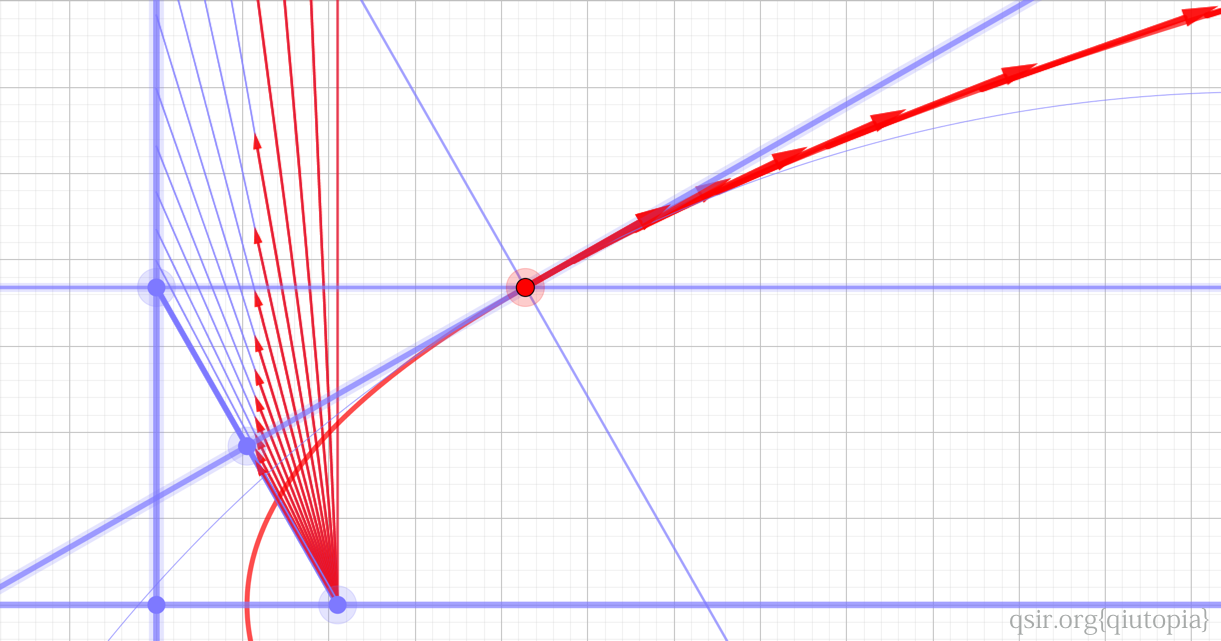
从速度向量平移共圆回归到共线，从焦点到圆（抛物线对应直线）上点连线长度成正比到成反比，没想到圆锥曲线的几何构造中，有那么简单和明显的速度关系...贪心了一点，根号二倍第一宇宙速度是脱离引力中心的最小速度如何用几何证明？

我们可以通过抛物运动的二级结论以及前面的探索结论，用物理的方法构造抛物线的焦点和准线（取抛物线上任意一点，做过定点对称轴的垂线，做顶点和垂足的中点连接抛物线上的点的直线为切线，过中点做切线垂线，交前面构造直线和对称轴，交点分属准线和焦点）。至于线段与速度垂直以及长度与速度成正比可以通过几何直角三角形和水平速度和竖直速度矢量三角形相似便捷给出结论...

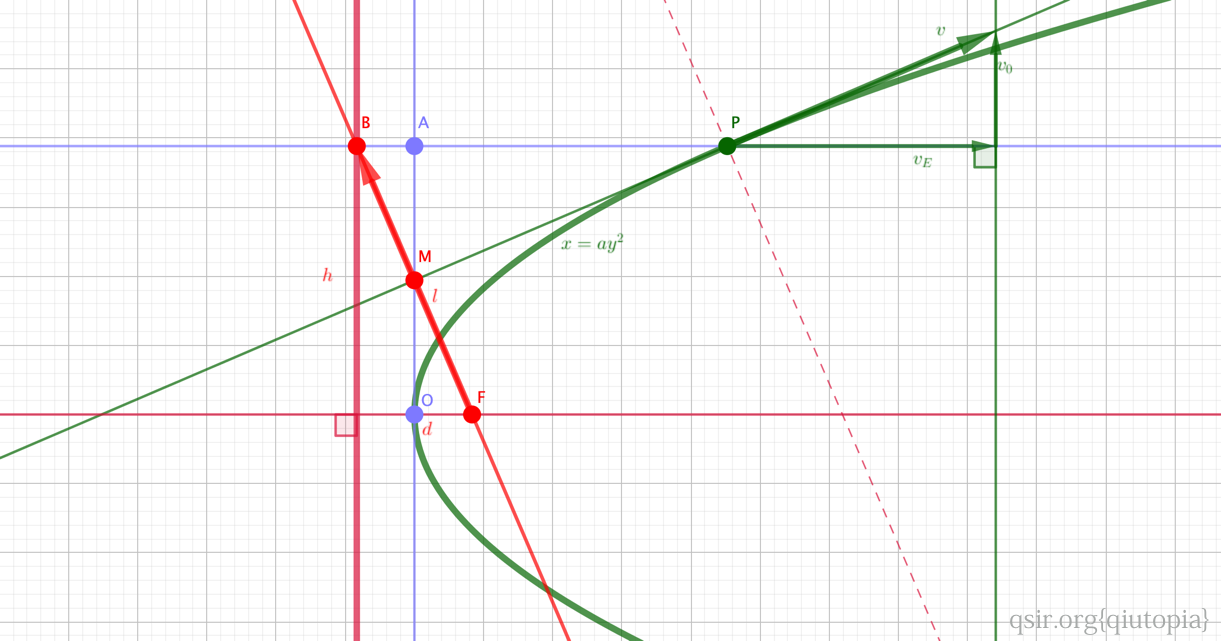
小结：圆锥曲线的三种（椭圆、双曲线和抛物线）不仅可以通过一种几何构造统一（利用圆上和圆内或外一点连线中垂线与过圆上该点直径交点，实现到两定点距离和、差为常数，以及利用一定点与一定直线连线中垂线与直线上该点垂线交点，实现到定点和定直线距离相等），而如此的构造模型中，和切线垂直的线段和圆锥曲线上动点速度的方向垂直，速度向量平移到虚焦点后共圆（圆周运动的速度共圆圆心在圆心，椭圆共圆偏心在圆内，双曲线共圆偏心在圆外）或共线（抛物线），且长度与速度大小正比（椭圆和抛物线）或反比（双曲线）...

以上探索最初的灵感来自Feynman's Lost Lecture (ft.3Blue1Brwon)[?]片段...

另，单一等同学已经在证明这些关系了，他数学知识有个用武之地了..."The scientist is not a person who gives the right answers, he's one who asks the right questions."理科老师的工作有时就很科学家哈哈~~~

[?]万年森等:有心力场速度矢量

On this day..

• Out of Our Minds - 2020
• 百分百糟糕的教育,巴西？ - 2012
• 一场无法扑灭的大火 - 2006
• 心花怒放之上海2005 - 2005
• 早退晚死 - 2005
• 上海往事 - 2005
• 教师是什么？ - 2004
• 喜欢做的事情自然有时间做 - 2004