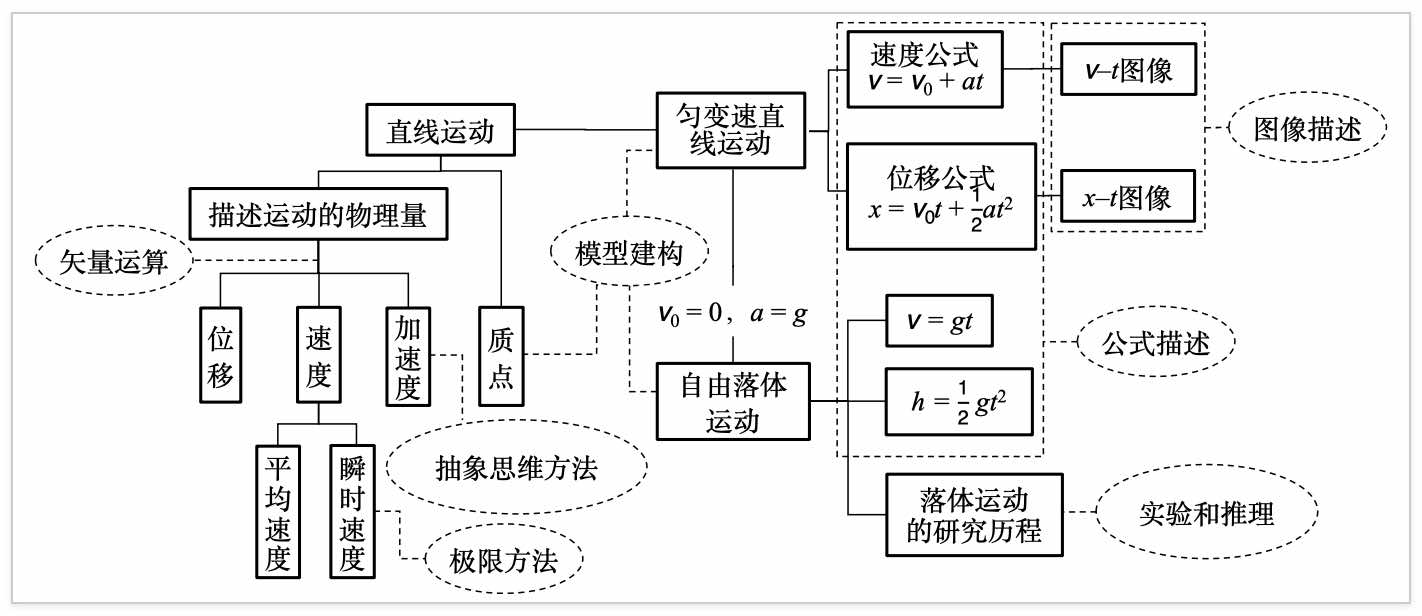
via[?]
一般性的匀变速运动中间时刻的位置与运行中点位置间的距离公式$\frac{1}{8}aT^2$（四种方法，代数法、中间时刻和中点速度公式、图像割补以及等分苹果$\frac{1}{2}a(\frac{T}{2})^2$）
p36纸带法绘制v-t图像。
导数和积分的问题可以结合到a v s 上。
p44光电门的应用。
光电门测加速度误差分析。测量值大于真实值
$a=\frac{(\frac{d}{\Delta t_1})^2+(\frac{d}{\Delta t_2})^2}{2L}$
频闪摄影
相对速度比速度合成更生活化。
a accelerationの頭文字
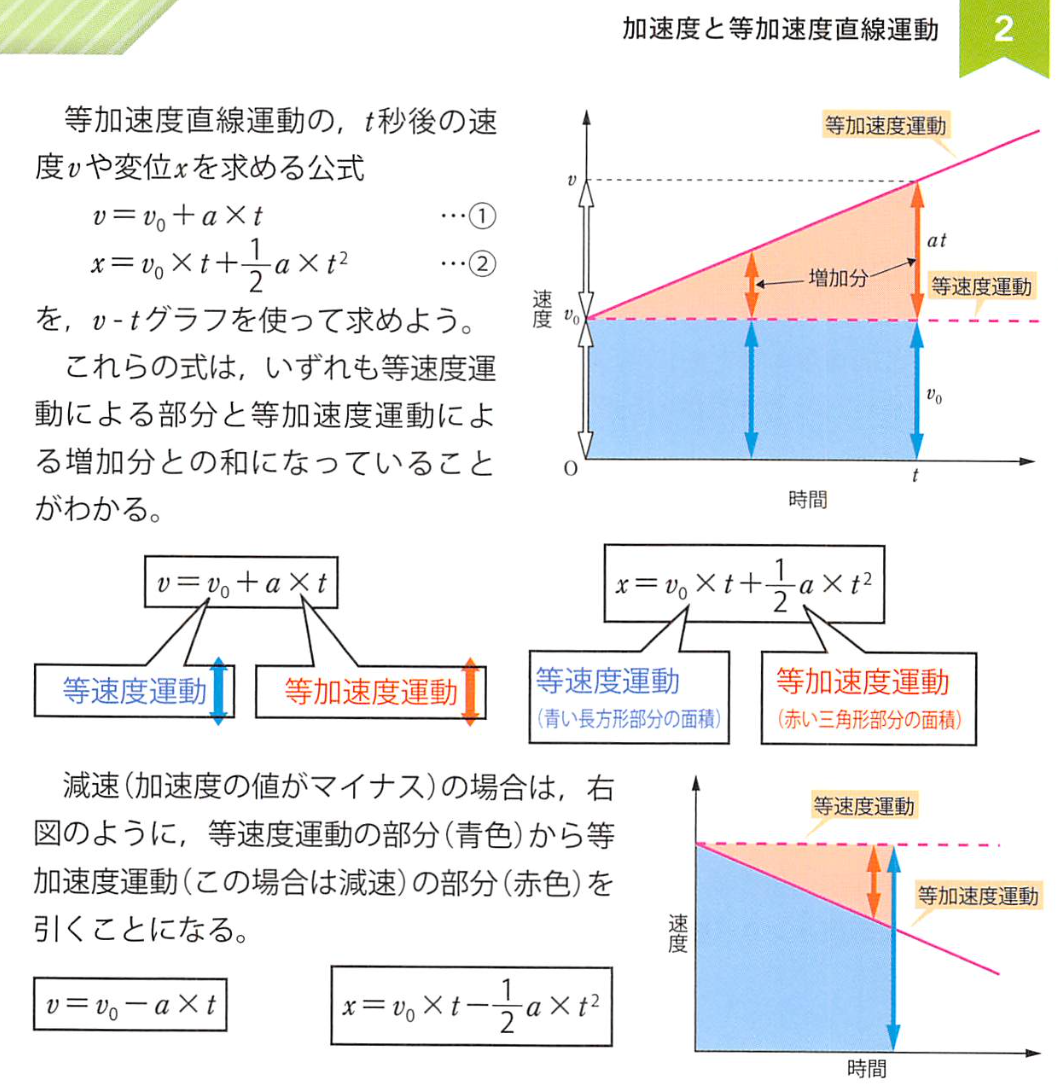
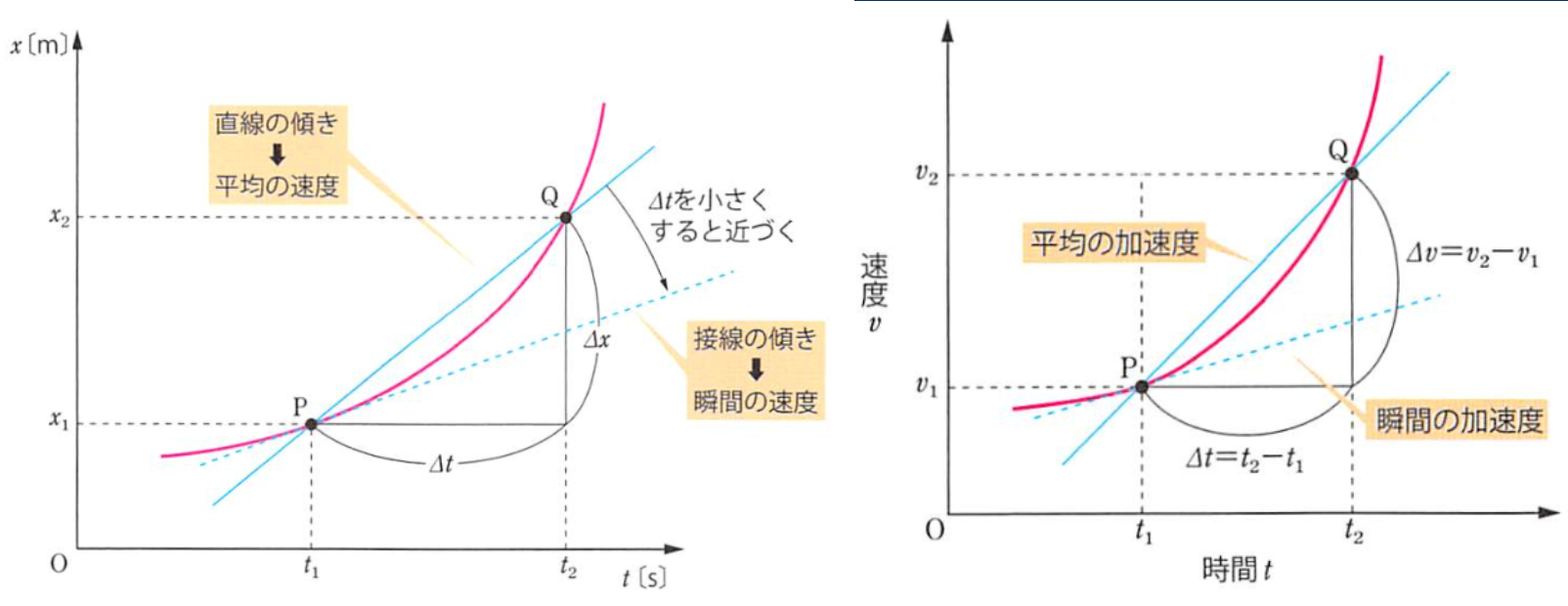
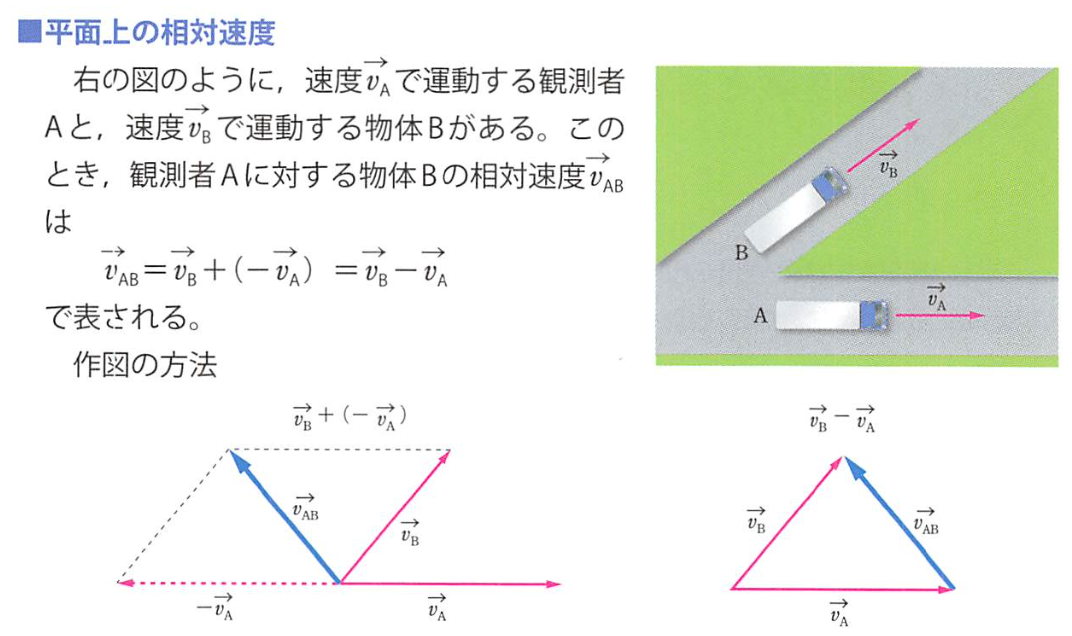
（公式增加动能变为一半（前后两个过程合外力的功一样）和动量变为一半（前后合外力的冲量一样））
（孙浚豪整理）运动学公式整理：
·基本公式：
$\bar{v} =\frac{x}{t} $
$v=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} $
$v={x}’ \left ( t \right ) $
$a=\lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} $
$a={v}’ \left ( t \right ) ={x}” \left ( t \right ) $
$v=v_{0}+at$
$x=v_{0}\cdot t+\frac{1}{2} at^{2}$
$x=v_{t}\cdot t-\frac{1}{2}at^{2} $
$x=\bar{v}\cdot t=\frac{v_{0}+v_{t}}{2} t$
$v_{t}^{2}-v_{0}^{2}=2ax$
$\bar{v}=v_{\frac{t}{2}} $
$\bar{v}=\frac{v_{0}+v_{t}}{2} $
$v_{\frac{x}{2}}=\sqrt{\frac{v_{0}^{2}+v_{t}^{2}}{2} } $
两个连续时间间隔T的位移差：$\Delta x=aT^{2} $
第n个T与第m个T的位移差：
$x_{n}-x_{m}=\left ( n-m \right )aT^{2} $
·初速度为0的匀加速直线运动：
前T时间内中间时刻位置与中间位移的距离：$d=\frac{1}{8}aT^{2} $
$T,2T,3T\dots \,nT$ 时间末物体瞬时速度之比：
$v_{1T}:v_{2T}:v_{3T}: \cdots :v_{nT}=1:2:3:\cdots :n$
$T,2T,3T\dots \,nT$ 时间内物体平均速度之比：
$\bar{v}_{1T}:\bar{v}_{2T}:\bar{v}_{3T}:\cdots :\bar{v}_{nT}=1:2:3:\cdots :n$
$T,2T,3T\dots \,nT$ 时间内物体位移之比：
$x_{1T}:x_{2T}:x_{3T}: \cdots :x_{nT}=1:4:9:\cdots :n^{2}$
物体通过$x,2x,3x\dots \,nx$ 位移末瞬时速度之比：
$v_{1x}:v_{2x}:v_{3x}: \cdots :v_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体通过$x,2x,3x\dots \,nx$ 位移所需时间之比：
$t_{1x}:t_{2x}:t_{3x}: \cdots :t_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体通过$x,2x,3x\dots \,nx$ 位移过程平均速度之比：
$\bar{v}_{1x}:\bar{v}_{2x}:\bar{v}_{3x}: \cdots :\bar{v}_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体经过连续相等时间内位移之比：
$x_{T_{1}}:x_{T_{2}}:x_{T_{3}}: \cdots :x_{T_{n}}=1:3:5:\cdots :\left ( 2n-1\right )$
物体通过连续相等位移所需时间之比：
$t_{x_{1}}:t_{x_{2}}:t_{x_{3}}:\cdots:t_{x_{n}}=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):\cdots :(\sqrt{n}-\sqrt{n-1}) $
静止开始，物体通过连续相等位移平均速度之比：
$1:\sqrt{2}+1:\sqrt{3}+\sqrt{2}…\sqrt{n}+\sqrt{n-1}$
$x_n=v_0T-\frac{1}{2}aT^2+naT^2$
$v(t)=\sqrt{v_0^2+2ax(t)}+v_0$
$x(t)=\frac{v(t)-v_0}{2}t+v_0t+x_0$（从梯形面积的角度考虑）
另，为了更好理解$\Delta x=aT^2$，特别进行了表格训练（匀变速运动）…
[?]一道运动学题目的多种解法
逐差法如果碰到奇数段如何处理?舍小或 增中间.
刘代表对碰球相遇问题有个很好的 解释
对杂耍仍球的模型,图像是个不错的 方式
相对加速度的概念解决相遇问题很有效果；
对于空中相遇的问题，s-t辅助理解。
v相同距离最大或距离最小。
豪哥负责？
物体由静止开始匀加速直线运动，最开始一段时间x1，最后一段相同时间是x2，求整个过程的位移
抛体运动可以把$$X=v_0t+\frac{1}{2}at^2$$看成是矢量表达式就可。
“你家住在15楼，你在中午睡觉的时候，听到一直有水滴砸在14楼的雨棚上，这时你的睡意全无，心想，是谁家的空调水管没放好，你从床上爬起来，发誓要找出这个人是几楼的，你打开手机测了一下每一滴水经过你家窗户的时间是0.1s，你家窗户高2m，重力加速度取10m/s2，请找出是几楼的空调水管没放好，不要算错了，否则会导致邻里矛盾哦。”
设定高度
设定时间
设定速度
以及可以巧用$$x_n-x_1=(n-1)gT^2$$
200米跑的平均速度？求解的是平均速率
4✖️100米的平均速率是比100米的更大的（中间接力的有启动的速度）
BC
高三一模的选择，直接运算有点复杂，不少学生用特殊值。
x2-2×1=3aT^2算是aT^2的拓展。
贴近生活的物理题目
运动学小题目
巧用$$\Delta x= aT^2$$
运动学经典题目
一道题十种方法
http://www.qiusir.com/?p=18376
一道运动学题目的多种解法
小谢和小李想到等时圆，我则巧用平均速度
Gemini给出
高考物理运动学部分要求在保证准确性的前提下追求答题速度。熟练掌握并能直接推导、应用的“二级结论”，是提升解题速度的利器。
## 一、 匀变速直线运动的核心比例（初速度为零）
对于 $v_0 = 0$ 的匀加速直线运动（或反向看作 $v_t = 0$ 的匀减速直线运动）：
* **结论 1：等时间间隔的位移比**
连续相等时间 $T$ 内的位移之比为连续奇数比：
$x_1 : x_2 : x_3 : \dots : x_n = 1 : 3 : 5 : \dots : (2n-1)$
* **结论 2：等时间间隔的末速度比**
$1T$ 末、$2T$ 末、$3T$ 末 $\dots$ $nT$ 末的瞬时速度之比：
$v_1 : v_2 : v_3 : \dots : v_n = 1 : 2 : 3 : \dots : n$
* **结论 3：等位移间隔的时间比**
通过连续相等的位移 $x$ 所用时间之比：
$t_1 : t_2 : t_3 : \dots : t_n = 1 : (\sqrt{2}-1) : (\sqrt{3}-\sqrt{2}) : \dots : (\sqrt{n}-\sqrt{n-1})$
* **结论 4：等位移间隔的末速度比**
通过连续相等的位移 $x$ 末的瞬时速度之比：
$v_1 : v_2 : v_3 : \dots : v_n = 1 : \sqrt{2} : \sqrt{3} : \dots : \sqrt{n}$
## 二、 平均速度与特殊位置速度
* **结论 5：任意匀变速直线运动的平均速度**
一段时间内，平均速度等于初末速度的算术平均值，也等于**中间时刻**的瞬时速度：
$\bar{v} = v_{\frac{t}{2}} = \frac{v_0 + v_t}{2}$
* **结论 6：中间位置的瞬时速度**
一段位移 $x$ 的**正中间位置**的瞬时速度（方均根速度）：
$v_{\frac{x}{2}} = \sqrt{\frac{v_0^2 + v_t^2}{2}}$
* **结论 7：中间时刻与中间位置速度的大小关系**
无论是匀加速还是匀减速直线运动，中间位置的速度永远大于中间时刻的速度：
$v_{\frac{x}{2}} > v_{\frac{t}{2}} \quad (\text{仅当 } v_0 = v_t \text{ 时等号成立})$
## 三、 纸带与多过程问题（多用于实验与大题）
* **结论 8：逐差法核心公式**
连续相等时间 $T$ 内的位移差为恒量（打点计时器求加速度的根本）：
$\Delta x = x_n – x_{n-1} = aT^2$
若不连续则有：$x_m – x_n = (m-n)aT^2$。
* **结论 9：刹车问题的隐蔽陷阱（死时间）**
刹车到停止的总时间 $t_{\text{stop}} = \frac{v_0}{a}$。若题目问 $t > t_{\text{stop}}$ 时的位移，**切勿直接代入公式**，此时位移已恒定：
$x_{\text{max}} = \frac{v_0^2}{2a}$
* **结论 10：多阶段运动（双阶段模型）**
物体从静止开始先以 $a_1$ 匀加速，再以 $a_2$ 匀减速到静止，总时间为 $t$，总位移为 $x$，则最大速度 $v_m$ 满足：
$v_m = \frac{a_1 a_2}{a_1 + a_2}t \quad \text{且} \quad x = \frac{1}{2}v_m t$
* **结论 11：双阶段运动的时间与位移分配**
承接结论 10，加速段与减速段的时间和位移分配与加速度成反比：
$\frac{t_1}{t_2} = \frac{x_1}{x_2} = \frac{a_2}{a_1}$
## 四、 平抛运动的几何与动态特征
* **结论 12：速度偏向角与位移偏向角的关系**
平抛运动中，某时刻速度与水平方向夹角为 $\theta$，位移与水平方向夹角为 $\alpha$，则：
$\tan\theta = 2\tan\alpha$
* **结论 13：速度反向延长线过中点**
平抛运动中，任意时刻速度方向的反向延长线，必然水平切分其此时总水平位移的**正中点**（即 $x_{\text{延长线交点}} = \frac{1}{2}x$）。
* **结论 14：平抛速度变化量的方向**
任意相等时间 $\Delta t$ 内，速度的变化量 $\Delta v = g\Delta t$，方向**始终竖直向下**。
* **结论 15：斜面平抛的对角线相遇**
若物体从倾角为 $\theta$ 的斜面顶端平抛并落回斜面上，其落体时间仅与初速度和斜面倾角有关：
$t = \frac{2v_0\tan\theta}{g}$
* **结论 16：垂直撞击斜面的条件**
若物体平抛并垂直撞击到倾角为 $\theta$ 的斜面上，则落地时的速度方向与水平夹角为 $90^\circ – \theta$，满足：
$\tan(90^\circ – \theta) = \frac{gt}{v_0} \implies \cot\theta = \frac{gt}{v_0}$
## 五、 圆周运动与追及相遇模型
* **结论 17：追及相遇的临界条件（极值点）**
两物体在同一直线上运动，它们**距离最近、最远或恰好不相撞**的临界条件是：**两物体速度相等**（即 $v_1 = v_2$）。
* **结论 18：皮带传动与同轴转动模型**
* **同轴转动**：各点角速度相等（$\omega_1 = \omega_2$），线速度与半径成正比（$v \propto r$）。
* **皮带/齿轮传动（无相对滑动）**：边缘各点线速度大小相等（$v_1 = v_2$），角速度与半径成反比（$\omega \propto \frac{1}{r}$）。
* **结论 19：竖直圆周运动（绳/内轨道模型）的最高点临界**
能过最高点的最小速度（临界速度）：
$v_{\text{min}} = \sqrt{gR}$
此时弹力（或绳子拉力）$F_N = 0$。
* **结论 20：竖直圆周运动（杆/管模型）的最高点临界**
由于杆和管能支撑物体，能过最高点的最小速度：
$v_{\text{min}} = 0$
* 当 $v = \sqrt{gR}$ 时，杆对物体无作用力。
* 当 $v > \sqrt{gR}$ 时，杆对物体施加**拉力（向下的力）**。
* 当 $v < \sqrt{gR}$ 时，杆对物体施加**支持力（向上的力）**。 ### 💡 高考应试建议： 1. **小题直接用，大题写步骤**：在选择题中，这些结论可以帮你秒杀答案；但在计算题中，切记**不要**直接写“由二级结论得...”，而是要用最基本的公式（如 $v=v_0+at$ 或 $x=\frac{1}{2}at^2$）作为前置推导，把二级结论作为你心中检查结果的底牌。 2. **结合 $v-t$ 图象**：大部分直线运动的二级结论（如比例、双阶段运动）在 $v-t$ 图象上都能转化为几何面积或斜率关系，结合图象记忆更不易出错。
4班温8童鞋提供一道运动学小题目
第一眼很简单，再想挺麻烦，细看，前两段位移比1:4，必然匀加,$a_1=1$，而最后两秒和最初两秒对称，两端加速度也同，然后根据总位移总时间求解···
纸带拼接的实验分析
足球，第一秒7.8m，第二和第三秒一共5m，足球的加速度-3.6
用图像，假定时间，横轴纵轴比例计算。
推荐一个题目：）
浚豪推荐
后两种方法是两个还没有升入高中的男孩的创意