\教的风险\学的错误\教学勇气- visible teaching and learning
虹桥中学青年教师交流会
PDF:认识我们的影响力 (926)
大家好,
Continue reading »

关于800多项关于学业成就的元分析的综合报告
Visible Learning: A Synthesis of Over 800 Meta-Analyses Relating to Achievement
John Hattie
约翰·哈蒂著 彭正梅等译

对学业成就影响最大的因素是教师,学校系统的影响相对较小。也就是说,学生上什么学习并不重要,遇到什么教师才是最重要的。显然,效应量较大的课程和教学,也与教师密切相关。因此,我们似乎可以宣称,不要谈论学校,教师才是最重要的因素!哈蒂吧古希腊“认识你自己”的格言改为“认识你自己的影响力!”哈蒂的《可见的学习》就是要传递“教师及其反馈的力量”。
教师在教授知识内容时,要思考和监测学生如何熟悉和精通这些新知识,如何构建这种认知和理解的概念。这就意味着帮助教师从学生的视角审视学习,同时也意味着学生要从教师的视角来看待自己的学习。也就是说,只有存在这种双重的“看待”时,才会实现哈蒂所期望的可见的教和可见的学。
教师中心的教学或直接教学法的效果要比国内课程改革专家所认为的要更好。
波普尔指出,“理论是一张网,我们把它抛出去,为了捕捉“世界”---也就是使世界合理化,得到解释和统治。我们正努力把网眼越织越密。”
对中国教育学者来说,尤其令人警惕的是,这种对我们自己教育方式的实证捍卫,竟然不是来自中国。(我们面临的问题是不计后果,这算不上好。)
前言
我们常常羞于使用“卓越”一词,因为我们认为学校里的卓越是不可能达到的。实际上,卓越是可以达到的:有很多卓越的例子,有些稍纵即逝,有些却积累下来。当卓越发生的时候---它真的会发生---我们需要给予它更高的评价,去承认它和推崇它。
1、挑战
在教育领域中,一个最为持久的观点就是“一切都似乎有效(everything seems to work)”。我们很难找到认为自己是处于“平均水平之下”的教师。(为师者大)
根据著名的变革理论专家的说法,我们的学校所面临的重要的问题之一,“不是抵制革新,而是由于不加批判和未经协调地接受过多的革新而造成的碎片化、负担过重和不连贯”。与其说教育缺乏好项目的供给,不如说缺乏对好项目的需求。也就是说,我们总是不断提供新的项目,而不是孕育对好项目的需求。
课堂教学怎么和200年前没有两样呢。(不会是因为有了网络课程才有的新冠吧)
增加反馈之前,重要的是要注意课堂氛围,会因为关键要确保“错误”是受欢迎的,“错误”是改善学习的主要手段。
过去200年的教学历史证明,教师关注的焦点持续集中在“什么起作用”的观念上。这种什么起作用的观念很少具有高水平的解释效力。
我们中那些不愿意把他们的观点放置到被反驳的危险中的人们,实际上还没有参与到科学的游戏中。
2、证据的本质:元分析的综合
一个有教养的人的标志在于...他会在每个领域内寻求其对象的本性所允许的精确。亚里士多德
家庭作业对学业成就的影响,确实随着年龄的增大而提高。
garbage in garbage out
提升学业成就最有效的一个影响因素就是反馈。(以前有说“针对性训练”)
霍桑效应:当本人意识到自己受到他人关注时会有更为优异的表现。
对教师最重要的建议是,给学生界定清晰的学习任务、掌控班级最重要的活动和测验,以及增加反馈,会产生很多益处。但与课堂重组相关的政策并没有得到很多支持。
Marzano(2000)提出,80%的学业成就变化来自于学生的影响,7%来自于学校的影响,13%来自于教师的影响。之后,他使用这些估算分别评价了在无效的、一般的、优秀的学校中,无效的、一般的、优秀的教师对学生学业成就的影响。尽管他认为一般的学校和很一般的教师没有多大危害,但是对学生学业成就分布的相对位置影响也很小;无效的教师,无论在多么有效的学校当孩子哦该,都对所有学生的排名有负面影响;而优秀的教师,即便在无效的学校,其学生也能保持或提高学业成就,这是非常明显的。“教师的杰出表现不仅仅弥补了很一般学校的表现,甚至也弥补了无效学校的表现。”
几乎所有因素都起作用。教育中90%的效应量都是正向的,10%是负向的,这其中大约一半是“预料中的”(比如爱捣乱的学生的影响);因此,我们所做的事情中大约95%对学业成就都有正向作用。当老师认为他们对学业成就起正向作用时,或者当一项政策能提高学业成就时,这几乎是一种平庸之见:实际上几乎所有的因素都起作用。只需要一次推动,我们就能提高学业成就。
教师发现布置家庭作业的效果不像许多提倡者或研究者所承诺的那样效果明显。
3、论点:可见的教和可见的学
我们在普遍性中进行思考,但却生活在细节之中。怀特海 1943(类似的话,正着活,倒着想。)
当教师成为他们自己教学的学习者,学生成为他们自己的教师的时候,对学生的学习就会产生最大的效果。当学生成为自己的教师的时候,他们就会表现出自我调节的特征,这对学习者来说是最可取的(自我监控、自我评估、自我评价、自我教学)(求师得)
一个安全的环境是欢迎并鼓励错误的---因为我们能从错误和反馈中学到很多,这些反馈产生于错误的学习方向,或者没有完全因循正确的学习方向。同样,教师自己也需要处于安全的环境中,学会如何成功,或者从其他人那里学习教学方法。
热情是学校教育最具有价值的成果之一。
在成功的教师和学生的课堂上,教和学是可见的;当成功的教和学发生时,在教师和学生表现出的热情里,教和学是可见的;教和学需要教师和学生具备很多技能和知识。教师必须知道学习何时是正确的或者错误的;学会何时进行实验,并从实验中学习;学会监控、寻求并给予反馈;当其他学习策略不起作用时,知道尝试新的学习策略。最重要的是,教学对于学生是可见的额,学习对于教师是可见的。越多的学生成为教师、越多的教师成为学生,结果就越成功。
这种对于可见的教的解释涉及将教师看成促进者、审慎的变革者以及学习的指导者。
教师永远不必想办法往课程中注入更多的思考,那就像是试图向夏尔巴搬运工的生活中再加入有氧运动。
过度学习---足够的熟练程度会带来其他理想成果。
当任务对于学生来说非常复杂的时候,元认知技能,而非智力,就成了学习成果的主要决定因素。
学校的影响通常被夸大了,尤其是在发达国际。
“油漆式改革”
学生是非常优秀的评价者,能做出准确的评价,辨别经验丰富的专家型教师和有经验但非专家型的教师。
我们不应当忽略那些无疑是最有资格评价教师的人---天天与教师在课堂上共处的学生。
如果教师在安全的、充满关怀的环境中与同事讨论教学问题,那么就会实现效果的最大化。
上课的目的是让学生积极参与到学习过程中---通过教师和其他人的行为---直到学生成为他们自己的教师,找到学习新材料和新观点的最佳方法,寻找资源帮助自己学习,以及设置一系列适当的核较为有挑战性的目标。
4、来自学生的影响
马太效应,富者愈富
先前成就d=0.67
皮亚杰提出的认知发展阶段(感知运动阶段、前运算阶段、具体运算阶段和形式运算阶段。)与学习成就之间有非常高的相关性。
贯穿本书的一个观点是,清晰的学习目的、明确的成功标准以及使学习能被学生看见,是使学生参与学习的关键因素。
对数学、科学的态度0.36;减少焦虑0.40;注意力、参与度0.48;动机0.48;自我概念0.43;人格0.19;自评成绩1.44;皮亚杰项目1.28
对认知和快乐之间的关系进行了研究,平均效应量0.53,表明长期处于快乐和良好的情绪状态下的人更可能有创造力和成为高效的问题解决者。
体育健身与认知功能的发挥之间相关性较弱,但却是正向的。
5、来自家庭的影响
学生学业成就与家长受教育程度之间的效应量0.60,与家长职业之间的效应量0.56,与家长收入之间的效应量0.58(学前教育项目0.45,早期干预0.47,对种族的积极态度0.32,性别0.12,药物0.33,锻炼放松0.28,饮食0.12,少生病0.23,早产儿体重0.54)
家庭结构0.17
家庭环境包括家庭当中社会心理和智力激发方面的测量0.57,电视0.18,家长参与0.51,
6、来自学校的影响
发达国家中许多真正对学生学习起作用的影响来自学校内部,来自特定教师、特定课程与教师所使用的教学策略的影响。
寄宿学校0.05,学校规模0.43(规模太大太小都会降低办学效益)
暑假-0.09,学生流动-0.34,校外课程经验0.09,学校领导者0.36,开放班级0.01,能力分轨0.12,班内分组0.16,小组学习0.49,留级-0.16
加快学习进度
对特殊班级资优学生的另一种教学方法是通过课程加快学习进度,“加速教学能让聪明的学生与智力相当的同伴共同完成与其能力相符的徐色系任务。”尽管还有很多可选方法,比如课程压缩或浓缩,或开设大学预修课,但通常是通过加快课程的徐色系进度或者让低年级徐色生提前学习高年级的课程来促进资优学生的学业进步。
进度加快的学生和其所升入的同年级聪明的学生取得的学业成就相同。进度加快的学生会有更高的教育志向,但在参与学校活动的比率方面没什么不同。
没有研究表明拓展学习内容比加快学习进度更有效;拓展学习内容在最好的情况下只是提供了抵制无聊的一种手段。
为什么这么多人抵制加快进度。这通常是因为人们对学习进度加快的学生的社会和情感认可程度以及有时间安排障碍方面的偏见和非理性看法。
加快进度不会使学生在社会和人际交往方面受益。
资优生即便加快进度能产生影响,也是能产生积极的社会影响,但不加速回造成消极影响。
(东北育才四十年的优才教育很大程度上得益于“高速度高难度高起点”---也就是加快学习进度---的教育策略的坚持,而社会补习机构对学生的积极面,也不是在拓展,而是在进度的提前,不少学生开学前就学完了一学期的内容...)
我们应当质疑不加快学习进度对资优学生造成的负面社会影响。
课堂管理0.52,课堂凝聚力0.53
学业成就与凝聚力、满意度、任务难度、规章制度、目标方向以及物质环境之间呈正相关,而学业成就与冲突、小团体主义、冷漠和秩序混乱呈负相关。成人之间的合作有助于提高学业成就、建立积极的人际关系以及获得社交支持和自尊。
同伴影响
尽管同伴很少参与教学与学习过程,但同伴影响的作用相当大。
友谊在课堂环境中的作用重大,因为友谊通常包括更高层次的关怀、支持和帮助,有助于解决冲突。
从学校层面分析,校服政策对学业成就的各个方面都造成了消极的影响。
7、来自教师的影响
目前那种认为教师对学生的学业成就起重要作用的颂歌具有误导性。不是所有的教师都会起作用,不是所有的教师都是专家。
学校内部的因素,特别是教师的质量,比校际的因素对学业成就变化的影响要大得多。
教师影响的变化对数学的影响远比对阅读的影响大。
“在社会经济地位低的学校,一个孩子拥有什么样的教师更重要。”
教师教育学院中最好的部分是教学实践,或者说在教学实践中才发生真正的学习,这正是由于教师教育学院中的理论学习经历缺乏效果。
教师教育的核心任务必须是改变这些现有的观念。
学校学科不仅仅包括他们作为学生时所学的事实和规则,教学中还有很多复杂和模糊的东西需要学习;教学不仅仅是一些零碎的个人技艺技能和常识;有很多教学观念他们可能从来都没有听说过;形成一种去控制学生行为的强烈愿望,会与很多教学观念的实施不相一致。
教师的学科知识影响教学效果的情况可能只是在某些基本技能水平上发生,而其后的影响会较小。
优秀教师对学生提出挑战、对他们具有较高的期望,鼓励学生进行学科学习,并且重视学科的表层和深层方面。
师生关系的效应量d=0.72
(我把试卷上出现 的错误视作育才堕落的标志。)
的错误视作育才堕落的标志。)
教师传达上课目的和成功达成这些目的的观念非常重要。
教师表达的清晰度,是教师在组织、解释、举例和指导练习以及评价血色好难过学习方面的语言清晰度,这是教师表达清晰度的先决条件。
如果教师运用特定的教学方法,对所有学生抱有高期望,与学生建立积极的师生关系,那么,其对学生学业成就的影响更有可能高过平均效应量。
8、来自课程的影响
视知觉项目0.55,词汇项目0.67,自然拼读教学法0.60,词语组合项目0.15,理解力项目0.58,反复阅读项目0.67,整体语言教学法0.06,置身于阅读中0.36,二次、三次机会项目0.50,写作项目0.44,戏剧艺术项目0.35,数学项目0.45,计算器的使用0.27,科学项目0.40,价值观、道德项目0.24,社交项目0.40,职业生涯教育项目0.38,综合课程项目0.39,知觉动作项目0.08,触觉刺激项目0.58,游戏项目0.50,创造力项目0.65,户外探险项目0.52,课外项目0.17
相比于教师用于事实课程的教学策略来说,课程内容对于学生借以获得的学习进步,没那么重要。
9、来自教学方法的影响(上)
先行组织者可以被“宽泛地定义为从读者原有的知识到应该学习的知识之间的桥梁;它们应该比具体的学习材料更抽象,更富包容性,并且为组织新材料提供工具。”
目标0.56,概念图d=0.57,提供形成性评价0.90,提问0.46,教师的即时反馈0.16,任务时间0.38,分散练习和集中练习0.71,
反馈是对学业成就影响最大的因素。
我们所犯的错误是把反馈当做某种教师提供给学生的东西。教师通常并未提供反馈,尽管他们声称一直在提供反馈。他们提供的很多反馈都是社会性的和行为性的。只有当我发现学生对教师的反馈的效果才是最强的时候,我才开始对他有了更好的理解。(每个人只有一次机会,大概就是关键反馈的效能。)
当教师寻求学生的反馈或者至少向学生的反馈保持开放时,也就是当教师了解这些来自学生的反馈,即学生知道什么、理解什么、错在什么地方、什么时候有错误的观念,以及在什么时候不够投入,此时教学和学习才能使同步和有效的。学生对教师的反馈有助于让学生可见。
把教学和反馈当成是一个连续体是很有用的。
当反馈与纠错评论相结合的时候,反馈和教学就交织在一起,直到“过程本身呈现出新的教学方式,而不是仅仅告诉学生正确与否。”
反馈是信息,凭借这种信息,学习者可以确定、增加、改写、调整或者重组他们记忆中的信息,无论信息是专业知识、元认知知识、关于自我或者任务的信息还是认知的技术和策略。
有形的奖励大大地削弱了内在动机,特别是对有趣的任务而言。
本书的一个主要观点是,给予教师有关在他们的课堂上正在发生什么的反馈是很有效的,这种反馈使他们能够确定“我怎样去”到达给学生设立的学习目的,这样他们就能够为学生决定“下一步去哪里”。
同伴指导
在课堂上由同伴做助教的总体效果是相当好。如果教育的目的是教学生自我调节并掌控自己的学习,那么他们必须从学生的角色转化为做自己教师的角色。
同伴指导对于那些指导者和被指导者都能带来许多学业的和社交的益处。
对于不同教学模式所产生的数学成就的效果所做的元分析中,Hartley 1977年发现,同伴指导师她所对比的不同条件中最有效的方法(d=0.60)。当用作对教师角色的补充而不是替代的时候,同伴指导是最有效的。跨年龄的指导者(0.72)比同龄的同伴(0.52)和成人指导者(0.54)能产生更大的效果。她也发现一个经普遍报道的结论:同伴指导对指导者的效果(0.58)和被指导者的效果(0.63)并没有太大差异。
当学生变成别人的教师的时候,教学者和学习者所学的一样多。当他们能够掌控或者自治这种教学的时候,效果更好。
“当我们教别人时,我们自己学的更多。”但是,一旦教师走进课堂并把学生当做教学和学习的接受着而不是生产者,他们显然已经忽视了自己的说法。
元认知是对思考的思考
元认知策略0.69,学习技能0.59,学习风格的匹配0.41,学生掌控学习0.04,
个性化教学与传统的讲授方式所产生的效果几乎相同(d=0.08)。
成功的学习基于价值性、清晰的学习目的,具体的要求和成功标准...
本章的中心思想是学习目的、成功标准,不但容忍而且欢迎犯错的课堂环境、对任务挑战性的关注、为减少差距而提供反馈,以及在学习任务中的满足感、进一步的投入、对成功的坚持不懈。
10、来自教学方法的影响(下)
教学策略0.60,交互式教学法0.74
交互式教学法是一种教给学生认知策略的教学过程设计,它可能会改善学生生的学习成果。
它强调的是让教师能够让学生学习和运用认知策略,诸如总结、提问、澄清和预测,而且这些事“通过学生与教师之间的对话来试图理解文本的意义而进行的”。这时候,每个学生摇身一变,成了教师,教师和学生经常轮流主持文本中一个小节的对话。
Adams and Engelmann(1996)在直接教学法和加速学习之间做了一个有益的联结。由于直接教学法的主要目标就是通过教学加速学生的学业成就进步,也就是说,在有限的时间里教更多的内容,其目的是超越死记硬背,促进概括和迁移,并且持续不断地监督学生的表现,使他们达成具有挑战性的目标。
动画的效果是优于静止图片的效果(d=0.46),但动画是用于装饰目的(d=0.29),还是用于呈现目的(d=0.89)---这是概念学习的关键,其效果大不相同。
归纳教学法0.33,探究式教学法0.31,问题解决教学法0.61,基于问题的学习0.15?
合作学习和竞争学习都比个别学习的方法更有效,这再次说明学习中的同伴的重要性。
合作学习0.41,合作与竞争学习0.54,合作与个别学习0.59,竞争与个别学习0.24,综合教学改革0.22,针对有学习障碍学习的综合干预0.77,合作教学与协同教学0.19,
同伴学习被充分利用时,使用计算机更有效。
反馈被充分利用时,使用计算机更有效。
基于网络的学习0.18,交互式视频法0.52,视听方法0.22,模拟0.33,程序教学0.24,远程教育0.09
如果没有教师参与,运用或不运用技术对学习也没有明显效果。
许多自上而下的改革,可能意味着教师没有评估这些改革对他们有没有作用。
11、结语:如何把所有这些放在一起
“要到哪里找回遗失在知识中的智慧?又到哪里找回淹没在信息中的知识?”Eliot,1934
研究中更为困难的任务之一是做出解释,而不是确定因果关系。
引领教育通往卓越的六个路标:
①教师是学习最大影响因素之一。
②教师需要发挥其指导作用,有影响力,有爱心,并且有积极参与到教与学当中的热情。
③教师需要注意到每一个学生的所思所知,并以此来建构意义和有价值的经验,精通他们所教的内容并有深度的理解,提供有意义和适当的反馈,使每个学生通过不同水平的课程获得持续的进步。
④教师需要了解他们课程的学习目的和成功标准,知道他们在多大程度上帮助所有学生达到这些标准...
⑤教室需要从单一观念迈向多元观念,并把这些观念联系起来然后予以扩展,使学习者能建构知识和观念。
⑥学校领导和教师需要营造一个良好的学校、办公室和课堂环境。
“当教师从学生的视角看待学习时,当学生从教师的视角看待自己时。”
教师的期望和观点必须经过争论、辩论和探讨。只有那样,学生的学业成就才会取得大的进步。
目前盛行的“反思性教学”往往忽略了反思需要基于证据,而不是事后将其合理化。
无论是对教师还是学生来说,学习都是个人的事情。
教师时如此有必要去花费更多的时间和精力,用学生的眼光去理解学习。
令人沮丧的是,“改革越是深入到学校教育的核心,就越不大可能对教与学产生大范围的影响。”

Visible Learning,即“可視化學習”(注:有些翻譯爲“可見的學習”,本文采用“可視化學習”)。
“The ‘visible’ aspect refers first to making student learning visible to teachers ……, also refers to making teaching visible to the student, such that they learn to become their own teachers.” (John Hattie, 2009)
“可視化”具有兩層含義:一是讓教師看見學生的“學”,教師能清楚得看到自己所起的作用;二是讓學生看見教師的“教”,促使學生逐漸成爲自己的教師。
學校將可視化學習具體闡釋到四個方面:想、看、問、聽。
想:自己設定學習目標,思考他們怎麼去學習,需要做什麼才能成功完成任務,如何去提高
看:看到有關他們學習的反饋
問:及時詢問遇到的問題,參與進學生間的討論
聽:傾聽來自同伴的想法或意見
John Hattie利用meta-meta-analysis將課室教學數據化...只有老師從學生眼中看見學習,同樣學生在老師看到自己,才是最有「效益」的教學。
如同書名Visible Learning,作者一直借用「眼睛」這個比喻來說明 老師應如何借用學生的眼睛來看待學習。
老師要養成「從 學生的角度」來看待學習的習慣,亦即從學生的角度來思考他們需要什 麼樣的學習任務才夠有挑戰性,也要思考他們需要什麼樣的回饋訊息才 能幫助他們有效進展──Hattie 認為「挑戰性」與「回饋」是學習歷程中的兩大關鍵元素。此外,老師也要教導學生能夠「看見自己的學習狀態」,如此才能培養他們成為具有終身學習、自律(self-regulatory)的學習者。這就是Hattie所謂「讓教與學都能被看見」(visible teaching and learning)的意思。
可見的學習(Visible Learning)是指通過可視化的方式,把學習過程中的各種信息、數據和結果展示出來,便於教學之間能更好地理解學習情況,並為學習提供直接回饋。-Edward de Bono
John Hattie 所著的《可见的学习》一书列举了138个影响学业成就的因素,「反馈」(Feedback) 位列前十位。 关于什么是反馈,Sadler 曾提出一个「差距」的观点:反馈的目的在于缩短学生「所在的此地」和他们「要去的彼地」之间的差距,即缩短先前或当前成就与成功标准之间的差距。
前十:
①1.44自评成绩、学生期望
②1.28皮亚杰项目
③1.07对干预的反映
④0.90教师的可靠性
⑤0.90提供形成性评价
⑥0.88微格教育
⑦0.82课堂讨论
⑧0.77针对残障学生的综合干预
⑨0.75教师的清晰度
⑩0.75反馈、回馈
11、0.74交互式教学
12、0.72师生关系
13、0.71分散练习和集中练习
14、0.69元认知策略
15、0.68加速学习
16、0.68课堂行为
新版:

https://visible-learning.org/hattie-ranking-influences-effect-sizes-learning-achievement/
https://www.visiblelearningmetax.com/Influences
https://ej.naer.edu.tw/JTR/v10.3/2017-12-jtr-v10n3-187.pdf
https://aplusala.org/best-practices-center/wp-content/uploads/sites/3/2019/02/Hattie-VisibleLearning-research-834.jpg

Learning to Teach, Teaching to Learn...

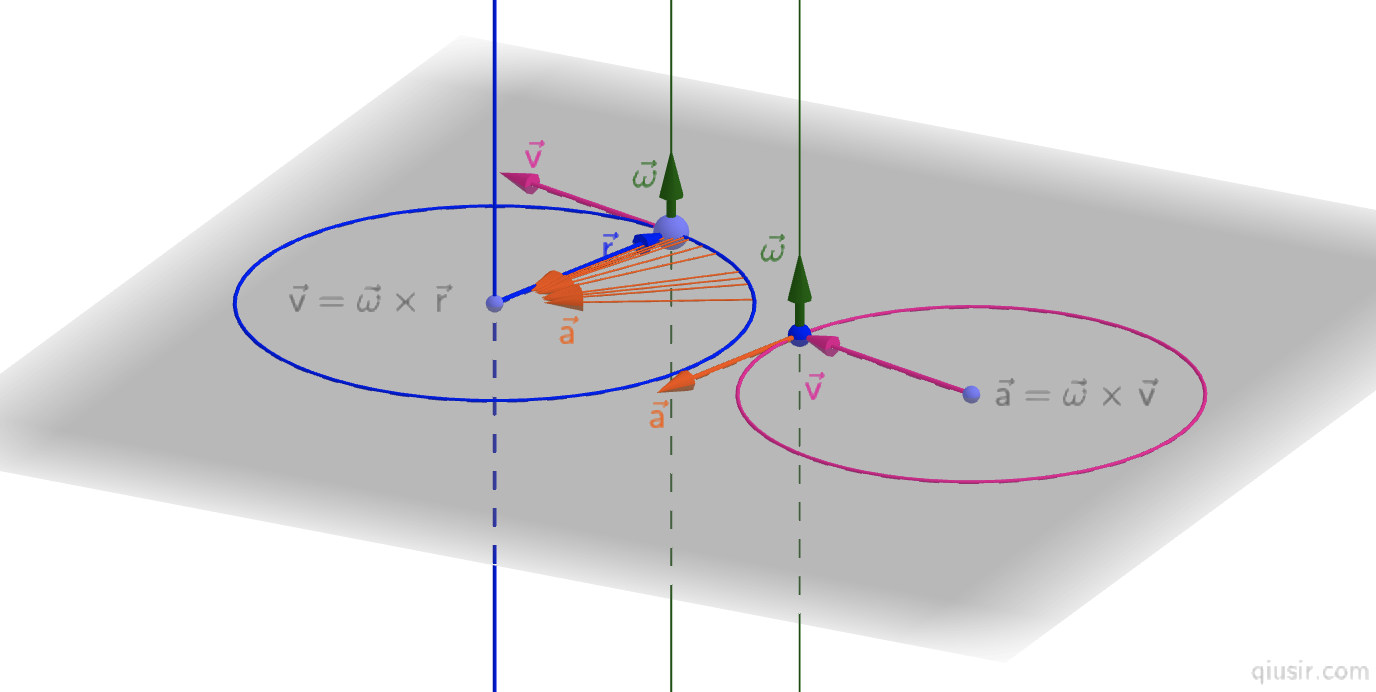
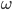 和线速度v分别和等速圆周运动的线速度v、角速度
和线速度v分别和等速圆周运动的线速度v、角速度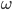 和半径r对应,
和半径r对应, ,
, ,既然
,既然 ,那
,那 。(
。( 是
是 关于时间的求导...)
关于时间的求导...)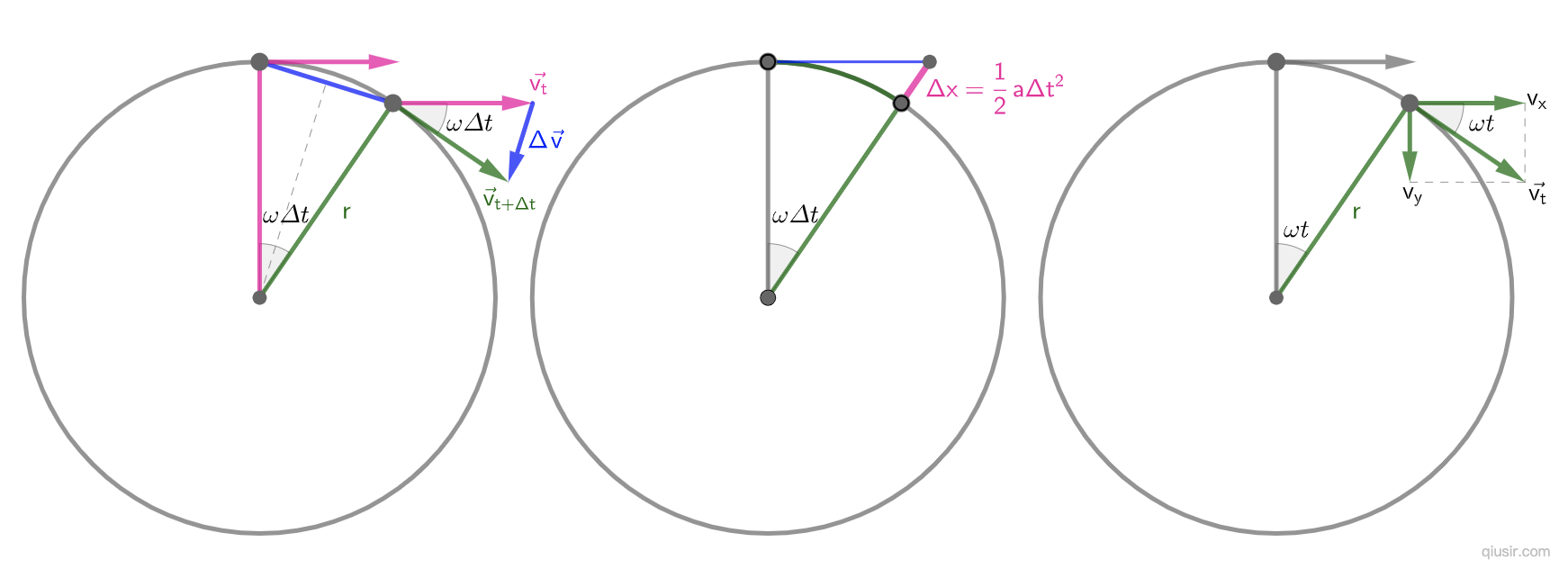
 ,
, ,
, ,
, ;
; 近似弦长,
近似弦长, ,
, ;
; ;
; ,
, ...
...
 ,
, ...
...
和前面不同,另一个思路是从运动叠加的角度推导向心加速度:
⑦这里可以顺便练习一下余弦的近似计算, ,
, ,
, ...
...
⑧同样是运动叠加,用勾股定理近似计算也可, ,简化处理,
,简化处理, ,
, ...
...
⑨对于上面的处理,孙浚豪同学是用移项后平方,高阶无穷小量消项。 ,
, ,
,
⑩用速度矢量的正交分解可关联到简谐振动, ,
, ,分别对时间求导得
,分别对时间求导得 ,
, ,
, ,和通常的极限法分析
,和通常的极限法分析 向心不同,这里可以直接得出加速度方向指向圆心的结论。
向心不同,这里可以直接得出加速度方向指向圆心的结论。
重新整理了这些对应试的意义不大,除了顺便用一下物理中偶尔用到的近似计算,大多数学生只关心结论就可以应付了,但对知识认知的层次是不同的。通常的中学物理教学,不仅对积分和导数的应用过分延后,对向量(矢量)的运算更是脱节,而且意识上的重视明显不够。
美国科学促进会(AAAS)1985年启动2061计划(哈雷彗星2061年会再次光临地球),帮助美国人提高科学、数学及技术素养,“美国历史上最显著的科学教育改革之一” ,号称“终极的科学计划” 。“既然数学对理解自然科学等具有中心重要地位,因而我们再次强调需要把数学与这些学科以综合的方式去教。综合的方法表明,一个现象的数学描述具有阐明和加强的效果。”
直接用加速度是位置矢量关于时间的二阶导数运算不香吗?有时更一般的方法反而会降低认知难度。
 ,
,

 ,
,

更一般:


对于等速圆周运动,



前面是对向心加速度的推导,而对它的理解大多局限在直接应用的层面,在FloatHeadPhysics频道上看到更直观的逻辑:
半径不变速度加倍,相同两个位置的速度变化量同样加倍,而所需要时间则因为速度加倍而减半,所以速度变化量应该是平方倍;同理,速度不变半径加倍,相同位置(角度)的速度变化量不变,而由于弧长加倍速度不变,所需时间加倍,那速度变化率减半。
特地找到杨振宁演讲的原视频截取了关于向心加速度的一段。因为战乱等原因,数学教授的儿子也没有学过高中物理,但似乎不妨碍他日后在物理学上的贡献。而现在的小朋友似乎学的有点多...
另,
发现有用 表示重力的,我觉得这样非常方面,和
表示重力的,我觉得这样非常方面,和 、
、 等表示一致,比用W表示更统一,特别是和万有引力常数G区分开。至于向心加速度,
等表示一致,比用W表示更统一,特别是和万有引力常数G区分开。至于向心加速度, 、
、 都可以,我更习惯弹力用
都可以,我更习惯弹力用 ,而向心力用
,而向心力用 ,都是normal...
,都是normal...
关于是匀速圆周运动还是等速圆周运动,个人更偏向台湾那等速圆周运动的称谓...
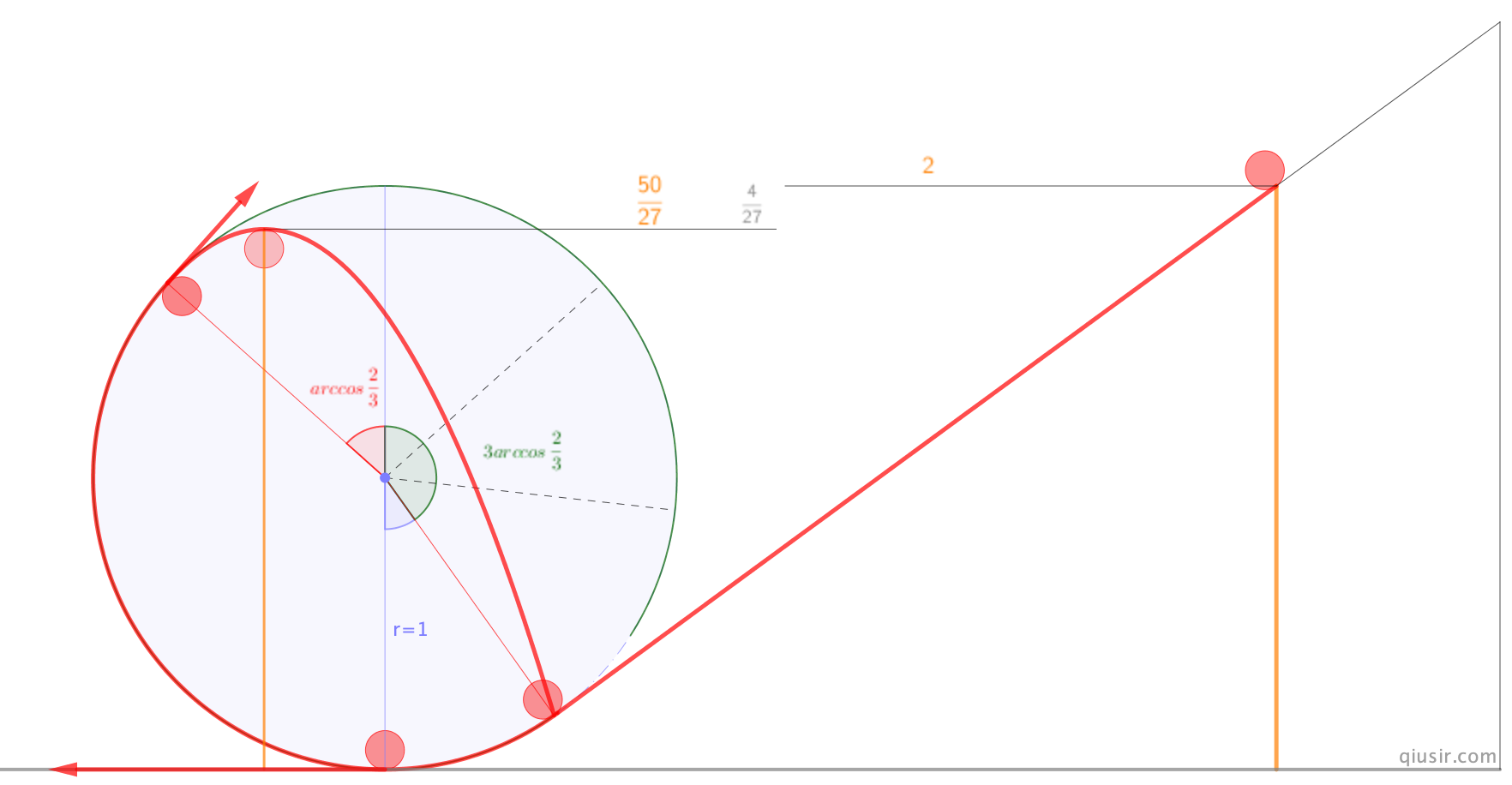
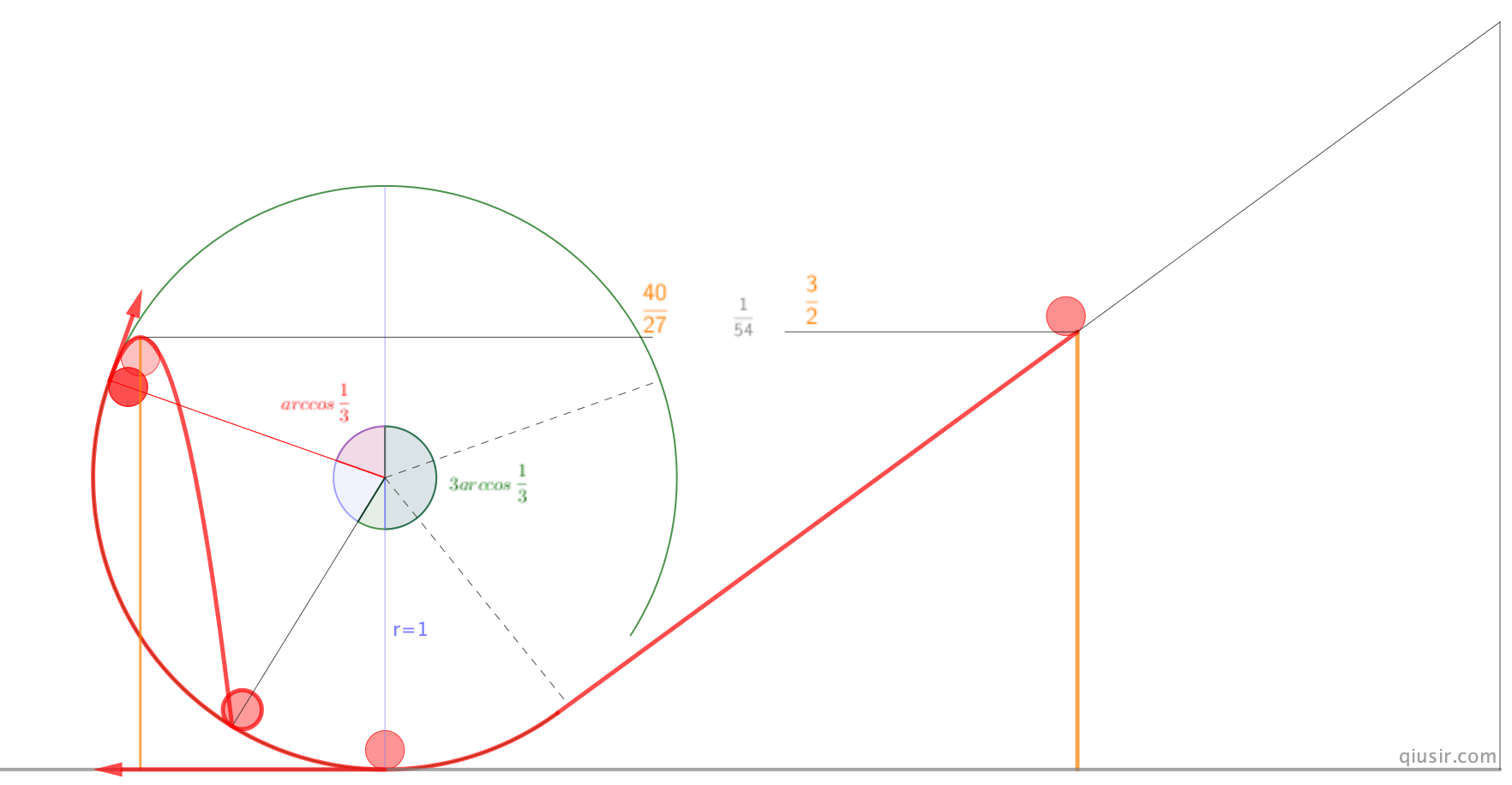
 ,最后为数不多的学生能继续计算,斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒,计算出
,最后为数不多的学生能继续计算,斜上抛的运动学角度或者求出抛体最高点动能再用机械能守恒,计算出 ...
...