JQX/进取芯 小教研第三期（2025.4.10）

简谐运动，作为高中物理力与运动的典型模型，揭示着振动世界的底层规律。
·如果弹簧振子不再处于理想光滑环境，摩擦力的介入是否会动摇简谐运动的本质？
·如果将弹簧引入含容单杆，在电磁力的动态影响下，振动方程将如何重构？
·如果单杆连接电感，电能与机械能的交替变化，会诞生怎样的新型简谐系统？
让我们一起深入探索不同的简谐运动，共同解构振动世界的「非理想」真相。

一、受外力的弹簧分离问题，一定能分离吗？
分离问题作为牛顿第二定律的基本应用，已经分析的比较透彻。但原本静止在弹簧上的两个物块，受到向上的恒力，一定能分离吗？让我们来分析这样一种情况：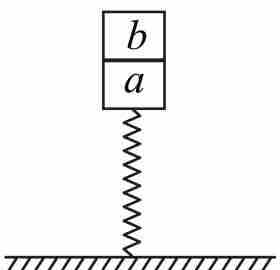
如图所示，一竖直轻弹簧静止在水平面上，重力均为$G$的$a$，$b$两物体叠放在轻弹簧上并处于静止状态，$a$、$b$可视为质点。问：至少需要多大的恒力$F$，竖直向上拉$b$，能使$b$与$a$分离？

答案：$F=\frac{2}{3}G$。

提示：根据分离问题的条件，分离时$a$、$b$两物体加速度相同，且物体间无压力。在有恒定外力$F$时，弹簧需达到压缩量为$\frac{F}{k}$的情况下，才可分离。

同时，根据简谐运动的对称性，受到恒力$F$可视为平衡位置上移$\frac{F}{k}$，由于初始状态为静止（即最低点），故此运动振幅为$\frac{F}{k}$。结合黑板中分析图，可知$\frac{2G}{k}=\frac{3F}{k}$，故$F=\frac{2}{3}G$。

肖老师提出，可以使用回复力的对称性，最高点的回复力应与最低点大小相同，算出合力。可见，恒力需要达到一定程度，才能将物块拉开，否则，物块将进行简谐运动不会分离。

二、水平弹簧振子，有摩擦，还是简谐运动吗？
如图所示，一轻质弹簧左端固定,右端系一小物块，物块与水平面的最大静摩擦力和滑动摩擦力都为$f$，弹簧无形变时，物块位于$O$点.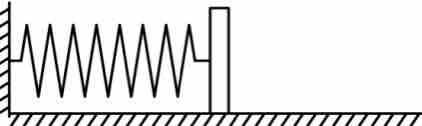每次都把物块拉到右侧不同位置由静止释放，释放时弹力$F$大于$f$，物体沿水平面滑动一段路程直到停止。为使物块能返回到$O$点右侧，则$F$至少为几倍的$f$？
答案：$F = 4f$。

提示：物块向左运动时，受到向右的摩擦$f$（可视为恒力），整个向左运动的过程中，可视为平衡位置为$O$点右侧$\frac{f}{k}$的简谐运动。同理，物块返回向右运动时，受到向左的摩擦$f$（可视为恒力），可视为平衡位置为$O$点左侧$\frac{f}{k}$的简谐运动。虽然整个过程不是简谐运动，但可以看做两个半程简谐的叠加。草图请见板书，根据对称性，可算得$F$为$4f$。

*这种阻力恒定的阻尼运动，可以视为每半程产生一次平衡位置的转移，导致振幅越来越小，直至恰好运动到或运动不到下次平衡位置转移的位置后，停止。

三、弹簧振子带动另一个物体运动，还是简谐运动吗？
如图所示（见黑板第二部分），质量分别为$m$、$M$的两个物块使用软杆连接，跨过定滑轮，$M$使用弹簧连接在地面上，从弹簧原长释放，试分析有$m$的存在，是否还是简谐运动，如果是，平衡位置、振幅、周期发生改变了吗？

答案：是简谐运动。不改变平衡位置、振幅。周期变小。

提示：可以使用整体法分析，$m$的存在单纯增加了质量，但未提供其他外力，外力依然为正弦变化，运动依然为简谐运动。平衡位置依然为弹力与$M$重力平衡的位置，振幅仍为原长到平衡位置。但由于$m$的存在，周期$T = 2\pi\sqrt{\frac{m}{k}}$,质量变大，周期变小。也可以使用单体法分析$M$，多受到一个杆的力，但杆力也为正弦力（相当于减小了$k$，而平衡位置未变）。

四、含容单杆增加弹簧，还是简谐运动吗？
如图所示，两条平行光滑足够长的无电阻导轨所在平面与水平地面的夹角为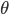$\theta$，间距为$L$。导轨上端接着没有充电的一平行板电容器，电容为$C$。导轨处于匀强磁场中，磁感应强度大小为$B$，方向垂直于导轨平面。在垂直于导轨无初速释放一质量为$m$、电阻不计的金属棒，若不计导轨电阻。金属棒与轻弹簧相连接，劲度系数为$k$，弹簧给金属棒的拉力垂直棒，静止释放时弹簧处于原长，则金属棒做什么运动？向下运动的最大位移是多少？

答案：做简谐运动。最大位移为$\frac{2mg\sin\theta}{k}$

提示：设下滑位移$x$时，速度为$v$，则$q = CU = CBLv$，
由牛二，$mg\sin\theta - kx - BIL = ma$，$I=\frac{\Delta q}{\Delta t}=CBLa$，解得$mg\sin\theta - kx - B^2L^2Ca = ma$
金属棒所受的合力$F=mg\sin\theta - kx-(m + B^2L^2C)a$
令$x_0=\frac{mg\sin\theta}{k}$，有$F=-k(x - x_0)$
故金属棒做平衡位置为$x_0=\frac{mg\sin\theta}{k}$，振幅为$A=\frac{mg\sin\theta}{k}$的简谐运动，向下运动的最大位移为$2A$，即$\frac{2mg\sin\theta}{k}$

*电容的存在，竟然并没有改变单独弹簧振子的平衡位置和振幅！
请进一步思考：
1）从物理意义上解释，平衡位置为什么是$mg\sin\theta$ ？
平衡位置应为$a = 0$，此处$I = CBL a$ ，$a = 0$ 没有电流故没有安培力，所以即为重力与弹簧弹力的平衡点。
2）最大速度能求吗？
可以考虑如下方法：①用简谐运动能量关系：$\frac{1}{2}kA^2=\frac{1}{2}mv^2$
②用简谐运动最大速度公式：$v_{max}=\omega A$……
3）继续考虑后半程，也是简谐吗？
后半程电容器放电，电流方向变化，所以安培力方向也发生改变，安培力大小依然与加速度成正比，方向与加速度反向，这相当于让加速度等比例减小（像等效质量一样，情景类似上上一道题，m换成等效质量的电容器……）（等效质量$B^2L^2C$在其他情境下亦有应用）， 只改变了$k$（也就是改变了周期和最大速度）。
4）有更方便的方法来计算最大位移吗？
末态$v = 0$，电容器没有电，利用能量守恒，可一步求解。
*肖老师提出，如果已知等效质量，那么可以直接整体分析……
*qiusir提出，电惯性、回复势能……

五、含电感的单杆问题，也是简谐运动？
如图所示，在磁感应强度为$B$且方向垂直向里的匀强磁场中，设有两条相距为$l$的固定光滑平行导轨，其与电感为$L$的线圈以及质量为$m$的横导杆构成回路。现给横导杆一个初速度$v_{0}$。若忽略所有元件的电阻以及电磁辐射的影响，试证明该横导杆的运动属于简谐运动。插

证明如下：根据法拉第电磁感应定律，感应电动势$\mathcal{E}=-L\frac{\Delta I}{\Delta t}$。
结合电磁感应现象 导体棒切割磁感线产生的感应电动势$\mathcal{E}=Blv$ ，同时电感的感生电动势$\mathcal{E}=-L\frac{\Delta I}{\Delta t}$ ，由于电路中没有电阻，有： $Blv=-L\frac{\Delta I}{\Delta t}$
两边同时乘以$\Delta t$ 并求和： $\sum Blv\Delta t=\sum - L\frac{\Delta I}{\Delta t}\Delta t$ ，得到： $Blx=-LI$
代入安培力公式   $F = B\left(-\frac{Bl}{L}x\right)l=-\frac{B^{2}l^{2}}{L}x$ 此式符合简谐运动回复力$F = - kx$ 的形式，从而可说明含容单杆的运动为简谐运动。

上述几类简谐运动不过是管中窥豹，自然界中满足回复力特征的运动远不止于此，还有无数未知的运动形式等待我们以更广阔的视角去探索发现！

【下期预告】
“Any fool can know, The point is to understand.”作为教师，知识的传授不单是传递和辅助理解，还有一个内化的过程。下次活动，qiusir将在新疆部高三的班级就“周期”的话题展开，除了相关知识的关联、拓展和内化，还有就如何和新同学进行有效交流的尝试等···

赵峥主编

（大学时上过赵教授的课，少有的印象深刻，大学同学间也常回忆起）
·[?]北京师范大学物理学系建立100周年庆祝会

“泛览周王传，流观山海图，俯仰终宇宙，不乐复何如。”陶渊明（欢言酌春酒，摘我园中蔬。接地气啊。）

“士不可以不弘毅，任重而道远。”曾子
01、文明的曙光
“上下四方曰宇，古往今来曰宙。”（我觉得最为神奇的古文）宇宙就是时间、空间和物质的总称。如果没有物质，也就没有了时间和空间。
文明的诞生，很像溶液中晶体的产生。只有当溶液饱和之后，才会有个别凝聚晶种成长起来。
古埃及人把一年定位365天，天狼星与太阳同时从地平线上升起来的那一天定为一年的开始。刚好也是尼罗河开始泛滥的日子。
德国商人谢里曼，特洛伊遗址
“全军出发，驴和学者在中间。”拿破仑
中国的诸子百家，单单缺少欧几里得这一家，这就为中国后来的落后，埋下了种子。
02、远古的辉煌
公元前584年5月28日希腊地区发生了日全食，泰勒斯早就预言这一天会发生日全食，这是人类对日全食的首次成功预报。
泰勒斯专心观察星空而不小心掉进井里，被一位女奴看见，笑他只关心遥远的天，却看不清脚下的地。
毕达哥拉斯最先使用“哲学”一词，首先认识到大地是球形的，最早提出“地球”的概念。
德谟克利特针对泰勒斯“万物源于水”的思想，提出了万物由原子组成。
柏拉图回到雅典开办了“阿卡德米Academy”，“不懂几何者莫入。”
欧几里得对托勒密国王说，“在几何学中，没有为国王专设的捷径。”
欧几里得对仆人说，“给他（一位刚入学的年轻学生）三个钱币，让他走，他居然想从几何学中捞取实惠。”
阿波罗尼对圆锥曲线的研究为2000年后开普勒发现行星运行定律打下了基础。
年轻的阿基米德曾在亚历山大科学院学习，和阿波罗尼一样，也是欧几里得的学生。
“不要动我的图！”
“五项全能”的埃拉托色尼人称β
公元529年，罗马皇帝下令关闭雅典的所有学校，包括柏拉图创办的那所已有900年历史的阿卡德米。
03、科学的诞生
公元前500年，毕达哥拉斯提出大地是球形的观点，我国汉朝也有“地如卵黄”的观点，不过主流是“天圆地方”。
公元前300年，亚里士多德系统提出地心说。
公元前200年，在亚历山大科学院工作的古希腊天文学家阿利斯塔克提出日心说。
公元100年蔡伦造纸，公元1150你啊传入西班牙。
“火药把骑士阶层炸得粉碎，指南针打开了世界市场并建立殖民地，而印刷术则变成新教的工具，总得说来变成了科学复兴的手段，变成对精神发展创造必要前提的强大杠杆。”
公元1487年，哥伦布发现美洲，以为是印度。
公元1521年，麦哲伦环球航行。
德国青年神学家马丁·路德在学会了拉丁文hou，发现民众由于不识拉丁文，看不懂《圣经》而被教会蒙骗···公元1517年，马丁·路德干脆将《圣经》翻译成德文···半个欧洲该信了信教（基督教）
“如果认为地球和行星都是绕着太阳运动，一起饿就变得简单而清楚了。”
布鲁诺进一步认为，宇宙没有中心，恒星都是太阳，更遥远的太阳。被监禁了7年，从不屈服，“我走向火堆，但你们比我更恐惧。”1600年，52岁的布鲁诺为科学和真理献出了自己的生命。
米开朗基罗逝世的1564年，莎士比亚和伽利略诞生。
把自己的发现用拉丁文写成一句话，然后把字母顺序打乱的“秘语”，既能保证发现的优先权，又能防止犯错的方法。

第谷原本在哥本哈根大学学习法律和哲学，由于有人预报了当时的一次日全食，使他惊讶不已，从此对天文学产生了兴趣并改学数学和天文。
1572年第谷发现了新星nava···丹麦国王怕第谷流失到德国，专门为他建立了一座天文台。第谷经过精密观测发现彗星的轨道不是正圆。第谷到德国工作了四年就去世了，他最大收获是得到了一个杰出的学生和继承人---天空立法者开普勒。
开普勒祖父是市长，父亲是职业军人，三岁得过天花，手和脚都有残疾，视力也不好···母亲被判女巫···
“我对老师（第谷）充满了尊敬，他是一位富翁，但不懂得怎样正确使用自己的财富。”“感谢上帝赐给我第谷这样的 老师，他是天才的观测者，正是这8分的偏差，引导我走上了改革整个天文学的道路。”（我对后半段的话存疑的，有点电影上“八年抗战开始了”）
伽利略最困难的时候，开普勒写信支持过他，“伽利略，鼓起勇气站起来，真理的力量无比强大。”
我曾测天高，如今测地深；灵魂飞向天国，肉体安详土中。
04、物理的初创
（除了把重物和轻物捆绑在一起的悖论）伽利略还有一个想法：大小相同的金球、铅球和木球放在水银里，只有金的下落；放在水里，只有木球漂浮；放在空气里，木球会慢一点。“鉴于这一点，如果完全排除空气阻力，所有的物体将下落得同样快。”
伽利略认为惯性运动是一种自由运动，静止和匀速直线运动属于惯性运动。伽利略还认为匀速圆周运动也属于惯性运动。他觉得行星绕日没有受到力，却能永远运动下去。长期以来，人们一直认为这是伽利略的一个失误，然而从广义相对论的角度看，伽利略把行星绕日运动看成是惯性运动的观点是正确的。爱因斯坦认为，万有引力不是真正的力，而是时空弯曲的表现。行星绕日就是弯曲时空中的自由运动（惯性运动）
行星绕日的轨道在三维空间中不是一个封闭的椭圆，在四维时空中，此轨道是测地线。
伽利略把匀速圆周运动看成是惯性运动的观点无疑是错误的，但他最终的目的是想说明行星绕日的运动是惯性运动，这一认识无疑是天才的和正确的。（那个年代对圆算得上是图腾了）
“卧看漫天云不动，不知云与我具东。”

英国的资产阶级革命爆发于1640年，清军入关是1644年，伽利略1642年1月8日逝世，这一年圣诞节，牛顿诞生在英国的一个农民家庭中···（正黄旗那小男孩记不住清军入关哈哈哈）
上帝、耶稣和圣灵三位一体的三一学院
牛顿用微粒说写成的光学论文，遭到胡克的批评，胡克支持惠更斯的波动说。
笛卡尔和惠更斯生活在伽利略和牛顿之间···
拉格朗日和哈密顿等人对经典力学进行形式上的改造，大量使用微积分，排斥初等几何。
H.Cavendish（W.Carvendish曾是剑桥大学校长，捐建卡文迪什实验室） big G 物理学中4个重要的普适常量，c\h\e
“神父并不像你想的那么聪明，我们无知才以为他们有学问。”（father teacher）
最多活一天的伏尔泰活到84岁，大半时间是在床上度过的，包括工作和写作。“更明智的做法不是卖马，而是把政府中的蠢驴裁减一半。”
提丢斯-波德定则。$R=0.3\times 2^{(n-2)}+0.4$ $dQ=TdS$ $dU=TdS-pdV$
提丢斯是一位中学教师，天文爱好者，发现太阳系各行星到太阳平均距离满足一个经验公式。
牛顿的生活由妹妹和外甥女照顾
门上开了一个洞供猫出入，后来大猫生了小猫，他又开了几个小洞供小猫出入
莱布尼茨死后，牛顿为伤透了莱布尼茨的心而洋洋自得。
（河滩上的石头，没有两块是一样的，但每一块又没什么不同。）

05、热学与统计
1775年北美爆发独立战争
纯铂米原器上刻写着“永远为人类服务”。
拉格朗日感慨，“砍下拉瓦锡的头只需一瞬间，但法国再过100年也难以长出这样的头。”
工业学校的学生要求参军保卫祖国，拿破仑没有同意，“我不能为取金蛋而杀掉我的母鸡。”
拉瓦锡死后，他的夫人改嫁伦福德。
开尔文即席评价了焦耳的工作，才使得与会者注意到焦耳的重大发现。
$dU=dQ-dW$
克劳修斯引进熵，时间流逝的方向就是熵增加的方向。
真实的自然过程都是不可逆过程。
开尔文24岁提出绝对温标
“我提出这些说法并不想争夺优先权，因为首先发表用正确原理建立的命题的人是克劳修斯···”
第零定律，热平衡的传递性
“热力学第一定律的发现者有三位，迈耶、焦耳和亥姆霍兹；热力学第二定律的发现者有两位，卡诺和克劳修斯；热力学第三定律的发现者只有一位，那就是能斯特。照此类推，热力学第零定律的发现者只能是零位。”
四大力学，理论力学、电动力学、统计力学和量子力学。
1895年，27岁的索末菲已经是著名的物理学家了，他写道：“玻尔兹曼与奥斯特瓦尔德之间的争论，仿佛是公牛与灵巧的剑手之间的角斗···我们这些年轻的数学家都站在玻尔兹曼一边。”
1900年M.Planck将玻尔兹曼揭示的熵与热力学概率的关系简化成$S=klnW$
k玻尔兹曼常数，W构成同一宏观状态的微观状态的数目
系统达到平衡后，宏观状态不再随时间变化，这时的宏观状态对应的微观状态达到极大值，也就是说熵达到极大值。
玻尔兹曼：“形式是否优美的问题应该留给裁缝和鞋匠去考虑。”
维也纳大学有玻尔兹曼、薛定谔、弗洛伊德和马赫等···
索末菲，熵比能具有更为重要的地位，熵决定了自然过程的时间箭头。
新陈代谢的本质是使有机体成功消除当它自身活着的时候不得不产生的全部的熵。
柏格森，“我们愈是深入地分析时间的自然性质，我们就会愈发懂得时间的延续就意味着发明，意味着新形式的创造，意味着一切新鲜实物连续不断地产生。”
城市也是一种耗散结构，是一个不断从外界输入“负熵”的开放系统。

06、认识电与光
1663年，“无形学院”被查理二世正式承认，胡克担任了皇家学会最早的总干事长。
胡克以发现弹性定律而著称于世，也是光的波动说的最早提出者之一，在胡克之前笛卡尔就主张光是波，与胡克同时代的惠更斯发展了光的波动理论。
胡克对牛顿的微粒说嗤之以鼻，不同意在皇家学会会报上发表，牛顿从此不再给皇家学会会报投稿。
英国人托马斯·杨2岁能读书，4岁通读《圣经》，14岁精通多种语言，后来在物理、化学、生物、医学、哲学、语言、考古等领域都有贡献。他认识到光是横波，提出了颜色的三色原理。（也有说是麦克斯韦的，他是发展和验证。）
法国人菲涅尔也独立对光的波动说做出贡献，与托马斯·杨相反，菲涅尔是一个显得迟钝的孩子，身体不好，曾因为反对拿破仑蹲过监狱，他靠自己的努力走进了科学殿堂。
托马斯·杨和菲涅尔几乎同时完成了光的干涉、衍射研究，他们并没有争夺发明权，而是互相赞美对方。（达尔文和阿尔弗雷德）
在惠更斯时代，丹麦人罗默通过对木星卫星的观察，测出光速。1676年
1986年规定1973年测定的光速值为精确值。
吉尔伯特，地球是一个大磁体，他还研究了摩擦起电，发明了第一个验电器。
出身一个铁匠家庭的法拉第，由于贫困和语音上的缺陷，收到老师嘲笑而离开了学校。
4小时的演讲稿编写成了380页的著作，烫金字的《戴维爵士演讲录》
戴维夫人拒绝与法拉第同桌，里夫教授非常愤慨，在另一个房间专门为法拉第单独设宴，以维护“一个不把别人的斤斤计较放在心上的、孤独的青年科学家”的尊严。

班里的同学看不起固执而孤僻的麦克斯韦，绰号“傻瓜”，三年后一次数学和诗歌比赛中，一举夺得两项第一···
$c_{em}=\frac{1}{\sqrt{\varepsilon_0\mu_0}}$
麦克斯韦用一个不正确的模型“推出了”正确的科学理论，就如卡诺从热质说推出卡诺定理一样。
自发辐射，处于高能级的原子，在没有受到外界影响的情况下，会有一定的概率从高能级自发地跳到低能级并发射光子。
受激辐射，当一个能量恰好等于两个能级差的光子如何过来时，会“刺激”处于高能态的和原子，使它跃迁到低能态，同时发射与入射光子同频率、同偏振、同相位、同运动方向的光子，近乎使一个光子变成了两个或多个相同的光子，使得出射光得到加强。（激光有很好的相干性。）
07、走近相对论
1900年，八国联军入侵中国的那一年；日本明治维新走上了富强的道路；1900年4月27日皇家学会迎接新世纪的年会上，开尔文勋爵两朵乌云的发言。
普朗克和儿子散步，这个发现如果不是错误的，将是非常重要的，也许能与牛肚的成就媲美。

德国中产阶级以上犹太家庭有一个传统，每周请一两个贫困犹太学生来家里吃饭。每次都带几本书给爱因斯坦···爱因斯坦有一个特点，能够长时间集中注意力，但记忆力差，总记不住单词和课文之外，老师尤其讨厌他居然敢打断自己讲话。没等爱因斯坦提交生病证明，校方主动找他谈话，劝其退学。16岁的爱因斯坦接受了校方的建议···

“（阿劳中学的补习班）用它的自由精神和那喜色好不仰赖外界权威的教师的淳朴热情，培养了我独立精神和创造精神。正是阿劳中学成为了孕育相对论的土壤。”

经过一年的补习，爱因斯坦终于进入苏黎世工业大学的师范系，闵可夫斯基（对爱因斯坦没什么印象）、韦伯（起初挺喜欢爱因斯坦，后来烦他不来听课）等著名教授都在那讲课。他愿意读一些名著而不愿意去听课。
爱因斯坦没能留校，米列娃只拿到结业证书。
“没有专利局对爱因斯坦更合适的工作单位了。”希尔伯特
爱因斯坦和几位热爱科学和哲学的好朋友组织了一个“奥林匹亚科学院”的小组
1905年，除了博士论文，爱因斯坦发表了4篇重要论文，①解释光电效应的论文，提出光子说；②关于布朗运动的论文，间接证明了分子存在；③《论运动物体的电动力学》，提出了狭义相对论；④提出质能关系式的论文，原子弹的理论基础。爱因斯坦很幸运，是普朗克审稿。
亚里士多德的以太理论
如果光速与光源运动有关，那双星中向着我们运动的恒星与背离我们运动的恒星发出的光的速度将不同，我们看到的双星轨道将会畸变，不再是椭圆。但所有双星的轨道并没有畸变。
1905年5月的一天，爱因斯坦拜访了好友贝索，奥林匹亚科学院的一员，经过一下午的讨论，爱因斯坦突然明白了，应该把光速不变看成一条公理。贝索一生都在听课、学习，还喜欢与人争论，与爱因斯坦的讨论，大大启发了爱因斯坦，尽管贝索并没有搞清楚，“阿尔伯特，你把我带进了历史。”
相对论的主要公式是洛伦兹变换，相对论的名字也是洛伦兹起的，但相对论的创始人却不是洛伦兹而是爱因斯坦。
一个质点描绘出的世界线的长度，就是它经历的真实时间，在相对论中称为该质点的硅油时间。
门捷列夫曾对燃油取暖的方式万分惋惜，“要知道，钞票也是可以用来生火的。”
$E_k=mc^2-m_0c^2=\frac{1}{2}m_0v^2+\frac{3}{8}m_0\frac{v^4}{c^2}+\dots$
$E^2=p^2c^2+m_0^2c^4$
能量和动量不可分割，也是一个整体，思维动量。
只有爱因斯坦一个人认识到“光速与观察者相对于光源的运动无关”，洛伦兹、庞加莱等都没有认识到这一点。（爱因斯坦感谢贝索在讨论中帮助了自己，尽管贝索感到茫然。）

08、弯曲的时空
“我实在无法赞扬你的儿子，因为赞扬他就等于赞扬我自己，我早就得到过与他相同的结果。”
$g$万有引力场强。
马赫关于惯性力与万有引力相似，都起源于物体间的相互作用的见解。爱因斯坦终于认识到，惯性问题应该和引力问题一起解决。

09、原子与核能
门捷列夫，俄罗斯人与梦国人的混血。门捷列夫因一票之差未能获得诺奖，当年的化学奖给了常压下石墨烧成金刚石的。此项假发现的学者并非蓄意造假，他坚信与金刚石化学成分相同的石墨，一定可以制成金刚石。但他的助手都不相信，他一炉又一炉地烧，都不成功。无法说服他又等得不耐烦的助手们在一次装炉时预先在里面放了一颗金刚石···他致死都不知道这实际上是一场恶作剧。（中国古代隐身草的翻版）
最初人们认为原子之所以能结合成分子，是因为原子间有万有引力，忽悠着原子带钩或环···瑞典的大学生阿仑尼乌斯认为是电磁力的结果。
居里夫人，由于营养不良，多次因贫血晕倒···
（1895德国伦琴发现X射线；1896法国贝克勒尔发现天然放射现象；1897年英国汤姆逊发现电子）不同于西瓜模型，日本长冈半太郎提出土星模型，带正电的实心球，电子像土星的光环一样绕原子旋转。
原子核物理之父卢瑟福，“我一生专门研究各种变化，但这次碰到的变化最大了，我在一夜之间从一个物理学家变成了一个化学家了。”研究生中11人获得诺奖，“诺贝尔奖得主的幼儿园”
泡利，“我从未听过比你更糟糕的报告”，转身对另一位年轻人说，“你那次在苏黎世的演讲除外”
精细结构常数$\alpha=\frac{e^2}{2\epsilon_0 h c}$ $\frac{1}{137}$
哈恩、迈特钠
“你和你的全家必须来领事馆做智力检测”，费米只好第二天带全家去美国领事馆···
费米一共培养了6位诺贝尔奖获得者。
奥本海默在德国哥廷根大学留学，与狄拉克是同班同学。
斯洛廷，勇敢的加拿大青年物理学家，用手将两块钚分开，实验室得救了，他让助手在黑板上记录下事故是每个人的位置，以便治疗时知道辐射的强度和不为，斯洛廷最终为原子弹制造献出了青春和生命。
氢弹的第一个设计者泰勒是杨振宁的博士生导师，一天十个主意，其中九个半是错的，
钱三强和何泽慧是约里奥-居里夫妇的学生。
约里奥托杨承宗带口信给毛，“要反对原子弹，必须自己有原子弹，原子弹没有那么可怕，原子弹的原理不是美国人发明的，你们忠狗不是也有自己的科学家吗？”（？）
1964年10月16日第一颗原子弹，1967年又成功引爆第一颗氢弹。
10、量子的世界
希尔伯特对物理学家的数学水平非常不以为然，“物理学对于物理学家来说，实在是太困难了。”
波恩的研讨班有一句名言：

愚蠢的问题不仅被允许，而且受欢迎。（不读书爱思考，是一种凡人病）

德布罗意最初申请参加索尔维会议被谢绝了···
本质上讲，生命需要的不是能量而是负熵。

11、粒子与对称性
1935年汤川秀树提出交换物质的思想来解释核力，获得1949年的诺奖。
汤川秀树是对近代自然科学做出重大贡献的第一位亚洲人。
12、恒星的演化
13、黑洞的启示
拉普拉斯等人根据万有引力定律和牛顿第二定律，得出暗星形成的条件

史瓦西黑洞
14、辽阔的星空
我们太阳系直径几乎达到一光年
海王星是用万有引力定律预言的
冥王星卫星的公转周期不仅与自己的自转周期同，还与冥王星自转周期同，是太阳系中唯一一个“三重同步”的天体。 北半球人肉眼可见的最远天体仙女座，距离我们22万光年。
红移，光源移动造成的多普勒红移，另一种是引力红移。大质量恒星表面附近，由于时空弯曲造成的红移。
15、宇宙的演化
16、时间的性质
公元前4004年10月22日下午8点，这一刻是时间开始的原点。（大主教根据路德和开普勒的研究）
1955年逝世之前，爱因斯坦再次重申，时空石物质伸张性和广延性的表现。他认为不存在一无所有的时空，没有物质就没有时空，时空与物质同存同灭。
热和引力是任何物质都有的来那个黄总最普遍的属性，而且，只有这两种属性是任何物质都有的，找不出第三种。
热与引力，是维持恒星和星系生存的一对矛盾，一个起排斥作用，另一个起吸引作用，最后达到一定的平衡。
引力不是真正的力，他不仅是时空的弯曲，而且与热不可分割。
第零定律表明时间是可以定义的；定义定律表明是时间是均匀的；第二定律表明时间流逝是有方向的；第三定律表明时间是无穷无尽的，既没有开始，又没有结束。（前面不太理解）
时间就像一条既没有源头，又没有终点的河流，向着特定的方向均匀地流逝着，远看起来，它十分平静，好像“长沟流月去无声”。但近看起来，会发现它有量子效应导致的涟漪、浪花、波涛与飞沫。

（中学时很喜欢，后来喜欢武侯祠“能攻心则反侧自消从古知兵非好战；不审势即宽严皆误后来治蜀要深思。”） 有志者事竟成破釜沉舟百而千关终属楚 苦心人天不负卧薪尝胆三千越甲可吞吴
$\frac{1}{2}mc^2<\frac{GMm}{r}$ $r< \frac{GM}{c^2}$

高三七的学生特地跑上楼来合影留念，一晃不到两个月他们就要考高了···

JQX/进取芯 小教研第二期（2025.4.7）

从感生电动势到参考系的变换---电磁感应的另一种打开方式

一、源起：一个关于涡流的疑问
在一次的公开课上，我提到一个与涡流相关的现象。题目中描述了金属铝片掠过凹槽装置的过程，铝片的运动速度逐渐减慢。讲课过程中对此的解释是：这是一种涡流现象，即在金属铝片中感应出了电流，铝片受到安培力作用，形成了一个阻尼力。
这本是教材中常规的解释路径——磁场静止，导体运动，从而形成闭合回路产生感生电动势。但在与邱sir和金老师的讨论中，发现在这个过程中，存在一个容易被忽视的概念性矛盾：
既然是金属铝片在运动，磁场不动，为什么不把这种情况归类为“动生电动势”呢？

教材的划分标准通常是：
导体相对于磁场运动、切割磁感线，属于动生电动势
闭合回路中磁通量随时间变化，属于感生电动势

磁场是静止的，导体在动，这不正是动生的定义吗？可为什么又以“感生”来处理？教材似乎默认了一个参考系（磁场所处的参考系），而忽略了不同参考系下对“感生”与“动生”的理解可能并不一致。
这让我们意识到：或许“感生”与“动生”的划分，并不是物理本质上的区分，而是参考系选择的结果。

二、初探：不同参考系下的电场与磁场
为了进一步理解涡流现象和感生与动生电动势的关系，我们先看一道沈阳市一模物理选择压轴题。
武汉智能电梯公司研制出世界第一台“磁悬浮电梯”，如图为该磁动力电梯的简易装置图，即在竖直平面内有两根平行竖直金属轨道MN和PQ，两轨道的下端用导线相连；金属轨道间有一导体杆ab与轨道垂直，其正下方通过绝缘装置固定电梯轿厢，设运动过程中ab始终与轨道垂直且接触良好。该磁动力电梯上行的原理是：电磁铁所产生的垂直轨道平面、磁感应强度为B的匀强磁场沿金属导轨运动，带动ab杆向上运动，即电磁驱动。设电梯轿厢及ab杆的总质量为M（后续简称电梯），两轨道间的距离为L，ab杆电阻为R，其余部分电阻不计。不计ab杆与轨道间的阻力和空气阻力，重力加速度为g。若电磁铁产生的匀强磁场以的速度匀速上升，电梯上升的最大速率为$v_m$，则下列说法正确的是（    ）
A．电梯刚向上启动时，ab杆中感应电流方向为b→a
B．电梯刚向上启动时，ab杆加速度
C．电梯以最大速率向上运行，ab杆产生的电功率
D．电梯以最大速率向上运行，外界在单位时间内提供的总能量

关于这道题目，我们还可以思考下面几个问题：
(a)ab杆中的电子受到的洛伦兹力的方向？
(b)ab杆中增加了重力势能和电能，那么洛伦兹力是否做正功了呢？
(c)导体棒开始的时候静止，那是什么力使导体棒中的电子运动的呢？
如果以磁场为参考系来观察，金属杆相对磁场向下移动。根据右手定则感应电流方向由b→a，导体棒受到安培力方向向上，由左手定则，导体棒中电子受到沿杆方向的 洛伦兹力方向向右。洛伦兹力可以看成两个分力，一个充当安培力做负功，一个充当非静电力做正功，洛伦兹力总功为零，这种情况下，不会出现矛盾。
然而，如果我们将参考系转换为地面参考系，问题就开始变得复杂了。由于金属杆向上运动，安培力向上，由左手定则，电流方向应该是由b→a。
但与此同时，如果我们试图使用电子所受洛伦兹力来分析，会发现负电荷所受的洛伦兹力方向是向左的，因此，感应电流应当是由a→b的。这时，两个不同的参考系下得到的电流方向显然不一致，带来了严重的物理矛盾。
电流方向作为客观现象，不应该随着参考系的不同而发生变化。那么，如何解释这个矛盾呢？
在进一步分析电流方向的问题之前，我们需要从电磁场的统一性出发，尝试找出解答这一矛盾的线索。众所周知，电场和磁场并非是完全独立的场，它们是同一种电磁场在不同参考系下的不同表现。通过对这两者的统一理解，我们可以有效消除由于参考系不同而产生的表面矛盾。

三、求索：非相对论角度的电磁场转化关系
为解决以上问题，我们需要从电磁场的统一性出发，分析电磁场在不同参考系下的不同表现。电场和磁场本质上是相互联系的，磁场和电场的变化，并不是完全独立的，它们通过洛伦兹变换在不同参考系下发生转化。
在不引入相对论形式体系的前提下，我们可以从基本的物理一致性出发，探讨电场和磁场在不同参考系下的转化关系。
首先，设想一个带电粒子在磁场中运动。由于洛伦兹力与粒子的速度相关，不同参考系中粒子的速度不同，因此磁场力的大小和方向也会不同。为了保证在不同惯性参考系中，粒子受到的合力保持一致，我们自然需要引入一个电场力项来补偿洛伦兹力的变化。这种思路反过来启发我们：不同参考系中观察到的电场，可能正是为了修正磁场力变化而“出现”的。
进一步地，我们思考电场如何转化为磁场。由于电场力与速度无关，难以用“力的补偿”来建立类比。但我们可以从电场的源头——静止电荷出发，考虑其在运动参考系中的表现。
假设空间中存在一条线密度为的线性排列的静止点电荷，产生沿径向分布的静电场。根据高斯定律，距线电荷垂直距离为r处的场强为：$E_0 = \frac{\lambda}{2 \pi r \epsilon_0}$

当我们切换到一个以速度沿导线方向运动的惯性参考系时，原本静止的点电荷对该观察者而言构成了一个线电流，等效地形成电流强度:$I = v_0 \lambda$

此时，根据安培环路定理，观察者在同样位置r处可以测得一个磁感应强度$B'$：$B' = \frac{\mu_0 v_0 \lambda}{2 \pi r}$
由$\mu_0 \epsilon_0 = \frac{1}{c^2}$，可以得到：$B' = \frac{v_0}{c^2} E_0$
这种等效电流所形成的磁场，本质上是“电场源”在相对运动下对观测者的“电磁表现”的改变。这一过程提示我们，电场的相对运动在某些条件下会表现为磁场，从而建立起了非相对论背景下的一种电磁场转化直觉。

四、明辨：相对论视角下的电磁场转换
尽管前面我们已经在低速近似的非相对论框架下进行了分析，但这些讨论依然无法完全解释某些电磁现象，尤其是在高速度或强磁场的情况下。为了进一步探讨电场和磁场在不同参考系下的转化关系，我们需要引入相对论视角。相对论不仅修正了空间和时间的关系，还使得电磁场的转换更加复杂，因此，在这种情况下，电场与磁场之间的转换规律会展现出更深层次的结构。
下面从相对论的角度分析电磁场的转换，首先在空间中设想一个最简单的电场：一个大的平行板电容器两板间的均匀电场。电容器在参考系中静止，电荷面密度为，由高斯定理可判断：$E_y = \frac{\sigma_0}{\varepsilon_0}$

参考系S以速度相对电容器像右运动，我们已经知道在参考系S中可以同时观察到电场和磁场。考虑相对论尺缩效应，面电荷密度变为：$\sigma =\gamma \sigma_0$。可求出S中场强为：$E_y = \frac{\sigma}{\varepsilon_0}$

由安培环路定理可判断：$B_z = -\mu_0 \sigma v_0$

我们设第三个参考系以速度相对运动，对于这个参考系中的电荷面密度为$\sigma' =\gamma '\sigma_0$。则对第三个参考系有：$E_y' = \frac{\sigma'}{\varepsilon_0}$ $B_z' = -\mu_0 \sigma 'v_0$
根据洛伦兹速度变换：$v' = \frac{v + v_0}{1 + \frac{v v_0}{c^2}}$

我们要做的是已知S系中的电场和磁场，如何求出系中的电场和磁场。也就是用E和B来表示$E'$和$B'$。$E'_y = \frac{\gamma}{\gamma_0} \frac{\sigma}{\epsilon_0}, \quad B'_z = -\frac{\gamma}{\gamma_0} \mu_0 \sigma v$
利用$\mu_0 \epsilon_0 = \frac{1}{c^2}$，通过数学运算可得到：$E'_y = \gamma \left( E_y - v B_z \right)$ $B'_z = \gamma \left( B_z - \frac{v}{c^2} E_y \right)$

如果将水平放置的磁场改为竖直放置，可推导出：
$E'_z = \gamma \left( E_z + v B_y \right)$ $B'_y = \gamma \left( B_y + \frac{v}{c^2} E_z \right)$
而平行于运动方向E与B的分量不变：$E'_x = E_x$ $B'_x = B_x$
用叉乘的方法可以使公式更为简洁：$\mathbf{E}' = \gamma \left( \mathbf{E} - \mathbf{v} \times \mathbf{B} \right)$ ${B}' = \gamma \left( \mathbf{B} + \frac{\mathbf{v}}{c^2} \times \mathbf{E} \right)$
我们可以看到，当我们变换参考系后，新参考系的磁场与原来参考系的电场有关。新参考系的电场与原参考系的磁场有关。因此，电场和磁场是不同参考系的两个投影，就像一个苹果，不同角度的人会看到不同的样子。

五、回眸：低速近似下的解答
在低速近似的非相对论框架下，我们来分析最初的高考问题：
(a)电流方向与洛伦兹力方向是否矛盾？
在地面参考系下，运动的磁场产生方向向左的电场：$\mathbf{E}' = -\mathbf{v}_0 \times \mathbf{B}$
导体棒中电子受到的合力为：$F = E'e - evB' = e(v_0 - v_m) B$
方向向右，这与磁场参考系下的结论一致。尽管电子受到向左的洛伦兹力，地面参考系中的电场力补偿了这一点，保持合力方向不变。
(b)洛伦兹力是否做功？
由于洛伦兹力始终垂直于电子的运动方向，它不做功。在磁场静止参考系中，垂直于杆方向的洛伦兹力做负功，沿杆方向的洛伦兹力做正功，总功为零。以地面参考系为例，充当安培力的洛伦兹力做正功，而沿杆方向的洛伦兹力和电场力共同提供非静电力，其中洛伦兹力做负功。总的来说，洛伦兹力做的功为零。
(c)导体棒开始时静止，是什么力使电子运动？
运动的磁场产生电场，电场力驱使导体棒中的电子运动。

六、结语：洞察、探索、卓越···
这一篇文章的思考起源于邱sir提出的一个问题——关于涡流现象中感生电动势与动生电动势的区别。正是这个疑问，激发了我和“jqx”团队的其他两位老师深入探讨电磁学中涡流、参考系转化等一系列问题。在这个过程中，我们三个老师的集体智慧与讨论让我对电磁场的理解更为深入，也让我在解答这一问题的过程中不断成长。
从最初的困惑，到逐渐明晰的解答，再到最终引入相对论的角度，这个过程充满了挑战与收获。

J - Judgment | Q - Quest | X - Xcellence

“jqx”这个小团体，通过洞察（Judgment ）发现问题的本质，依靠探索（Quest）勇敢追求未知，不断追求卓越（Xcellence），力求在每一领域做到最好。这三者相辅相成，推动着我们不断前进和超越！

【下期预告】简谐运动：当理想模型遇上阻力……
简谐运动，作为高中物理力与运动的典型模型，揭示着振动世界的底层规律。但当这个理想模型加上真实世界的约束，会发生怎样的物理剧变？
如果弹簧振子不再处于理想光滑环境，摩擦力的介入是否会动摇简谐运动的本质？
如果将弹簧引入含容单杆，在电磁阻力的动态影响下，振动方程将如何重构？
如果单杆连接电感，电能与机械能的交替变化，会诞生怎样的新型简谐系统？
下一期，让我们一起深入探索不同的简谐运动，共同解构振动世界的「非理想」真相！

昨晚回家雨夹雪···

一早散步，四班窗前小松鼠一家···

这个球的安放挺合我意···

河边看柳···

盛京龙柳0号[?]···

怒放的花儿啊，你们可曾想过我看落花的悲伤，这是犒赏还是惩罚···

“泛览周王传，流观山海图。俯仰终宇宙，不乐复何如？”赵峥教授的书上看到陶渊明这句，很带感。“我们不需要其他任何东西，活着，呼吸，迈出一步，就已经很美妙了。”