位移中点与时间中点的位移
最近才主要关于匀变速运动位置中点到中间时刻的位移的结论竟然如此奇妙: 。有了这个精简的结论,分析用光电门测量物体减速度的误差问题就要容易很多,而更值得珍惜的是这个认知过程中学生和老师的协力发展。
。有了这个精简的结论,分析用光电门测量物体减速度的误差问题就要容易很多,而更值得珍惜的是这个认知过程中学生和老师的协力发展。
已知物体匀加速通过两个距离为L的光电门,遮光片宽度为d,通过两个光电门所需时间分别是 和
和 。用这种方法测的加速度为
。用这种方法测的加速度为 ,而这个问题的难点是对于用这种方法测量加速度的系统误差是偏大还是偏小(忽略偶然因素的影响)。
,而这个问题的难点是对于用这种方法测量加速度的系统误差是偏大还是偏小(忽略偶然因素的影响)。
首先应该明确的是L是两个光电门的距离,也是两个遮光片中点处经过光电门的距离,而上述方法用到的速度是遮光片经过光电门的平均速度,也是中间时刻的速度,应该用中间时刻间的位移而使用的是中间位置的位移,这是系统误差产生的原因。
从应试看,毕竟只是一个二选一的填空,最初我只是采用近似法进行系统误差分析的,速度更快时经过光电门时,中间位置和中间时刻更接近,算是次要因素(也不严谨,尽管时间差小但速度差大)。从速度时间图像看,中间时刻间的位移大于中间位置的位移,所以系统误差是测得的加速度偏大。后来才注意到这本身就是一道很不错的运动学题目。
这几年大概有几个学生对这个问题有着自己很不多的探究。
崔家瑞
少儿班化学竞赛学生,求师得数位学习的大将。记得崔同学竟然设了四个速度,但结果又很简答,代数的力量感现在还有印象。为了简化,这里就分析经过第一个遮光片的情况就好。
初速度 ,末速度
,末速度 ,中间时刻的速度
,中间时刻的速度 ,中间位置的速度
,中间位置的速度 ,
,
 ,整理的,
,整理的,
张宸溪
直升班开朗的男孩,初三直升的学生有耐心用基本的公式进行运算,这是学生最应该用的方法。借助图像更容易理解。

整理后得,位置中点与中间时刻间的距离
阿布都旭库尔
肖遥老师在去食堂的路上和我说起新疆部有学生发现的一种方法,觉得很好,吃饭的时候还在讨论,的确很巧妙,而我的记忆力第一次出现新疆学生的奇思妙想,这算是我花时间整理这个知识点的动力之一。
他用到 ,即相邻时间间隔内位移差,而我们要求解的是中间位置和中间时刻的距离,应该是刚才这个差值的一半,即只有从中间时刻的位置后撤刚才的位移的一般才能保证是位置的中点。
,即相邻时间间隔内位移差,而我们要求解的是中间位置和中间时刻的距离,应该是刚才这个差值的一半,即只有从中间时刻的位置后撤刚才的位移的一般才能保证是位置的中点。
徐川皓
毕业许久的徐同学除了在说说上总给我点赞,还鼓励过我坚持自己的教育理想。我记忆中他可是很内敛的学生,而一次课上讨论这道加速度误差的问题,他想到的是面积割补的方法,现在印象还是深刻。中间位置与中间时刻的位移转化为中间时刻与速度轴的三角形面积,结论一目了然。
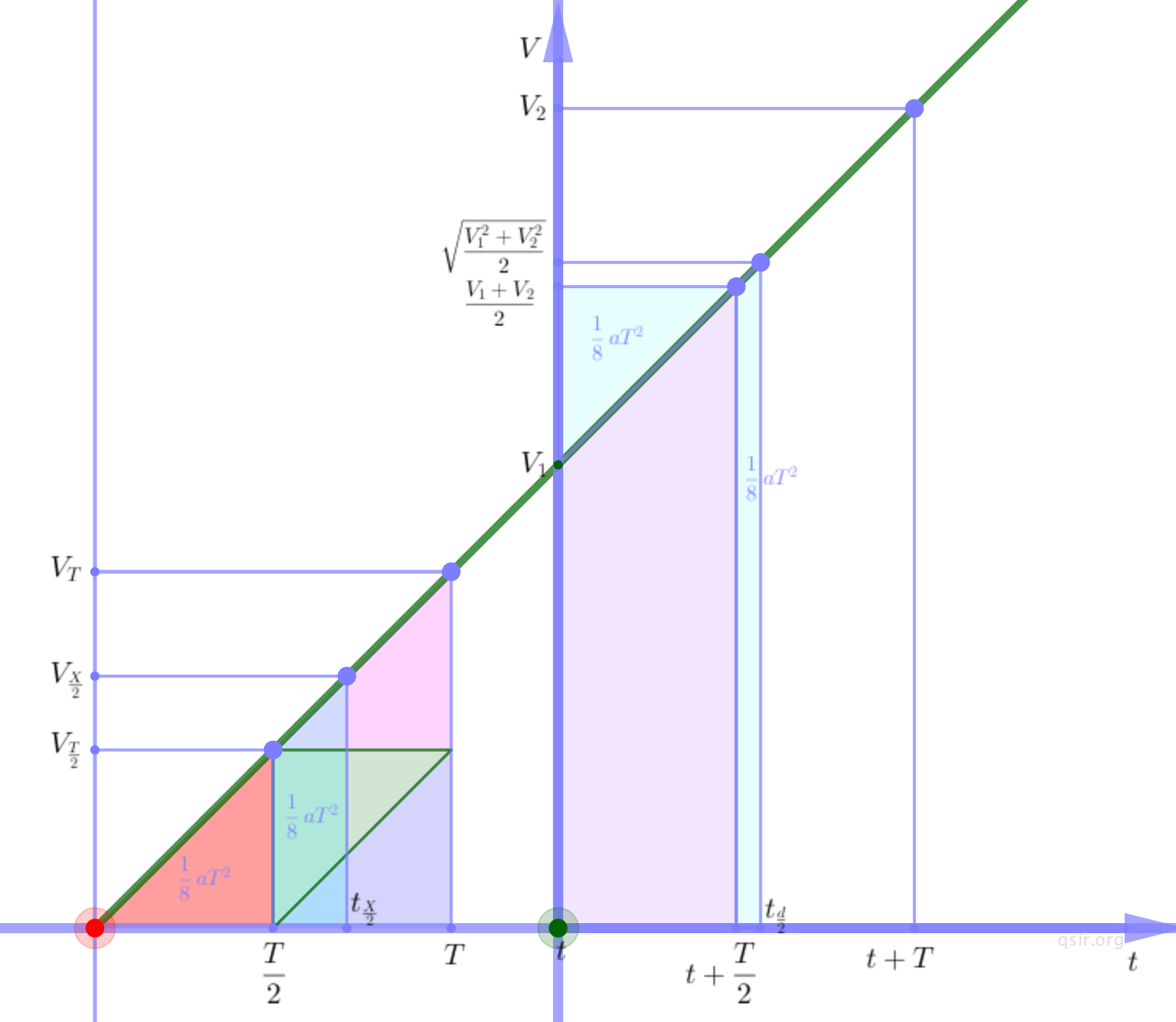
任泉羽
理科部学生会的“老干部”,学习踏实诚恳,这是可是学习品质中的大聪明,他对于特殊情况的分析其实也很有意义。就是如果初速度为0,前一半时间和后一半时间的位移是1和3份,而中点当然前后是2份,那中间时刻和中点的位移自然是1份了,也就是位移的
 ,从这个角度看,前面的结论可以看成是
,从这个角度看,前面的结论可以看成是 ,从一种特殊情况看到这个规律竟然有通用性。
,从一种特殊情况看到这个规律竟然有通用性。
边思羽
分别设定第一次遮光结束时的速度
 和第二次遮光结束时的速度
和第二次遮光结束时的速度 ,
, ,
, ,利用
,利用 ,并由前两式代入化简可得,
,并由前两式代入化简可得, 如果是测减速运动的加速度,结论相反。
如果是测减速运动的加速度,结论相反。
3月 10th, 2022 at 09:07
华胤实同学从整个过程的角度,以及摩擦力和重力作用时间的比例为定值两个点,就可以求出这个模型运动的总时间(碰撞时间忽略)(碰撞次数无穷多而时间是有限的...)(汪炳言和王云枫两位也主动计算了时间的问题)