三 27

雁过拔毛

教学|〖基础物理〗, 高三|〖苦海泛舟〗 qiusir 2010

中学物理的习题中经常出现子弹打木块的模型，说光滑水平面上有静止的木块M，被速度为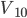V_{10}、质量为m的子弹击穿后，子弹和木块的速度分别为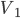V_{1}和V_{1'}...
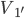这样的题目一般要分别以子弹和木块为研究对象，运用动能定理：
m: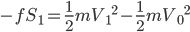-fS_{1}=\frac{1}{2}m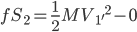{V_{1}}^2-\frac{1}{2}m{V_{0}}^2，
M:fS_{2}=\frac{1}{2}M{V_{1'}}^2-0。
两式相加得到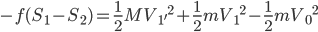-f(S_{1}-S_{2})=\frac{1}{2}M{V_{1'}}^2+\frac{1}{2}m{V_{1}}^2-\frac{1}{2}m{V_{0}}^2，
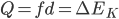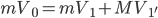Q=fd=\Delta{E_{K}}。以子弹和木块组成的系统为研究对象又有mV_{0}=mV_{1}+MV_{1'}。

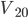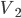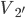若子弹的初速度变为更大的V_{20}射击同一木块，击穿后子弹和木块的速度分别为V_{2}和V_{2'}...设定子弹和木块的相互作用的力恒定。这里会有一系列的小问题：子弹速度增大后是否一定能击穿木块？若能够击穿，则击穿的时间如何变化？木块获得的速度或动能如何变化？子弹损失的动能如何变化？系统损失的动能如何变化？作用力的冲量如何变化？作用力对木块的功如何变化？子弹克服阻力的功如何变化...

m1ygbm.jpg

这些问题的求解一方面可以通过上述的代数式，更简洁的方式是通过V-t图直接分析...因为木块的厚度为定值，所以图中两个梯形面积相等，所以系统的机械能损失为定值，接下来一系列的问题迎刃而解...这里还涉及到一个有趣的话题，如果把子弹击穿木块后自身能量的减少比作雁过拔毛的话，如何让大雁的毛被少拔一些呢？结果是提高子弹自身的速度。

简单的几条线勾勒出子弹打木块的动态图景，而面积相等的一个等量却形象的表述出相关的参数关系，这样的图示即便是黑板上的简单线条，也能勾起头脑里的具体和丰富的想象。

On this day..

Comments are closed.