三 19

物理中常用的极值计算

教研|〖数理探究〗, 高三|〖苦海泛舟〗 qiusir 2010

时下（或一直以来）的物理教育早已摒弃了实验的基础，除了像是哲学的思辨外，更多时候成了应用数学的推演了。当然知识并无界限，所谓不同科目或许真的是为了将就人类的智商，但问题是长此以往，我们最多也只看到多面体的一面。嗯，现实就是一面的:)

中学物理的习题中经常出现一些极值讨论的问题，其中涉及到一些数学上的方法，比如点到直线的距离最短、二次函数求极值的方法、因式分解、三角函数和圆的几何性质等等，这些范例很能体现数学的工具性，除了拓展学生思维，也有利于数理的融合...

一、二次方程的判别式
选取适当的物理量，通过等式变换出现二次项，再利用判别式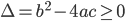\Delta=b^2-4ac\geq0作为有解的条件来求解。

二、二次函数的配方法
对于二次函数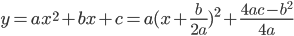y=ax^2+bx+c=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}
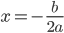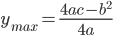若a<0，则y有极大值，当x=-\frac{b}{2a}时，y_{max}=\frac{4ac-b^2}{4a}；
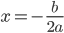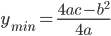
若a>0，则y有极小值，当x=-\frac{b}{2a}时，y_{min}=\frac{4ac-b^2}{4a}

题如匀加速与匀速运动的追击问题。
汽车在路口以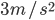3m/s^2 的加速度开始行驶，此时恰有一辆自行车以6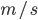m/s的速度匀速驶超过汽车。汽车从路口开动后，在追上自行车之前过多长时间两车相距最远？（2s，6m）

三、利用不等式
1.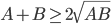A+B\geq2\sqrt{AB}：对正数A和B，若AB为常数，当A=B时，A和B的和有最小值。
2.AB\leq(\frac{A+B}{2})^2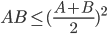：对正数A和B，若A+B为常数，当A=B时，A和B的和有最大值。
类似还有A+B+C\geq3\sqrt[3]{ABC}

题如水平释放悬挂小球重力最大功率位置求解。
一轻绳一端固定，另一端拴一小球，拉起小球使轻绳水平后无初速度的释放，小球在运动至轻绳达到竖直位置的过程中，小球所受重力的瞬时功率在何处取得最大值？
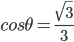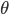（cos\theta=\frac{\sqrt3}{3}，\theta为线与竖直方向的夹角。）
此题目也可以研究竖直方向的受力情况，
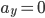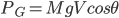当a_{y}=0时竖直方向的速度（V_{y}=Vcos\theta）最大，则P_{G}=MgVcos\theta取最大值。

四、三角函数
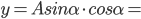
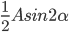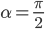简单一点的比如y=Asin\alpha\cdot{cos\alpha}=\frac{1}{2}Asin2\alpha，当\alpha=\frac{\pi}{2}取极值。
如在底边定长光滑斜面下滑时间极值求解。
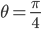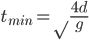如斜面底边恒定为d，当斜面与底边所成夹角θ为多大时，物体沿此光滑斜面由静止从顶端滑到底端所用时间最短? （\theta=\frac{\pi}{4}，t_{min}=\surd{\frac{4d}{g}}）

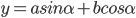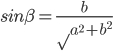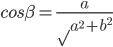
对y关于\alpha的函数，y=asin\alpha+bcos\alpha，令sin\beta=\frac{b}{\surd{a^2+b^2}}，cos\beta=\frac{a}{\surd{a^2+b^2}}
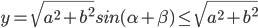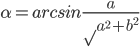则有y=\sqrt{a^2+b^2}sin(\alpha+\beta)\leq\sqrt{a^2+b^2}，当\alpha=arcsin\frac{a}{\surd{a^2+b^2}}时取等。

题如物体放置在水平地面上，与地面之间的动摩擦因数为μ，物体重为G，欲使物体沿水平地面做匀速直线运动，所用的最小拉力F为多大？
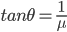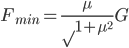（tan\theta=\frac{1}{\mu}，F_{min}=\frac{\mu}{\surd{1+\mu^2}}G）

五、矢量三角形
某一分力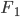F_{1}大小和方向定值，合力F的方向固定，则另外一分力有最小值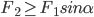，F_2\geq{F_1sin\alpha}
题如上面粗糙水平面匀速运动物体所收外力的极值问题求解也可以借鉴此法。

六、求导求极值问题
比如对二次函数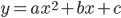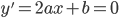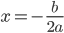y=ax^2+bx+c，y'=2ax+b=0，x=-\frac{b}{2a}时函数取极值。
如等量同种电荷中垂线上场强极大位置的求解。
对所得到得函数关于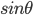sin\theta求导可得，当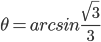\theta=arcsin\frac{\sqrt{3}}{3}时取极大值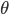，\theta为电荷与P点连线与水平方向的夹角。）
...
每一部分推荐的题目可以根据描述，自己画图推算，然后对照答案。\heartsuit
PS.常用数学符号的LaTeX表示方法

On this day..

Comments are closed.