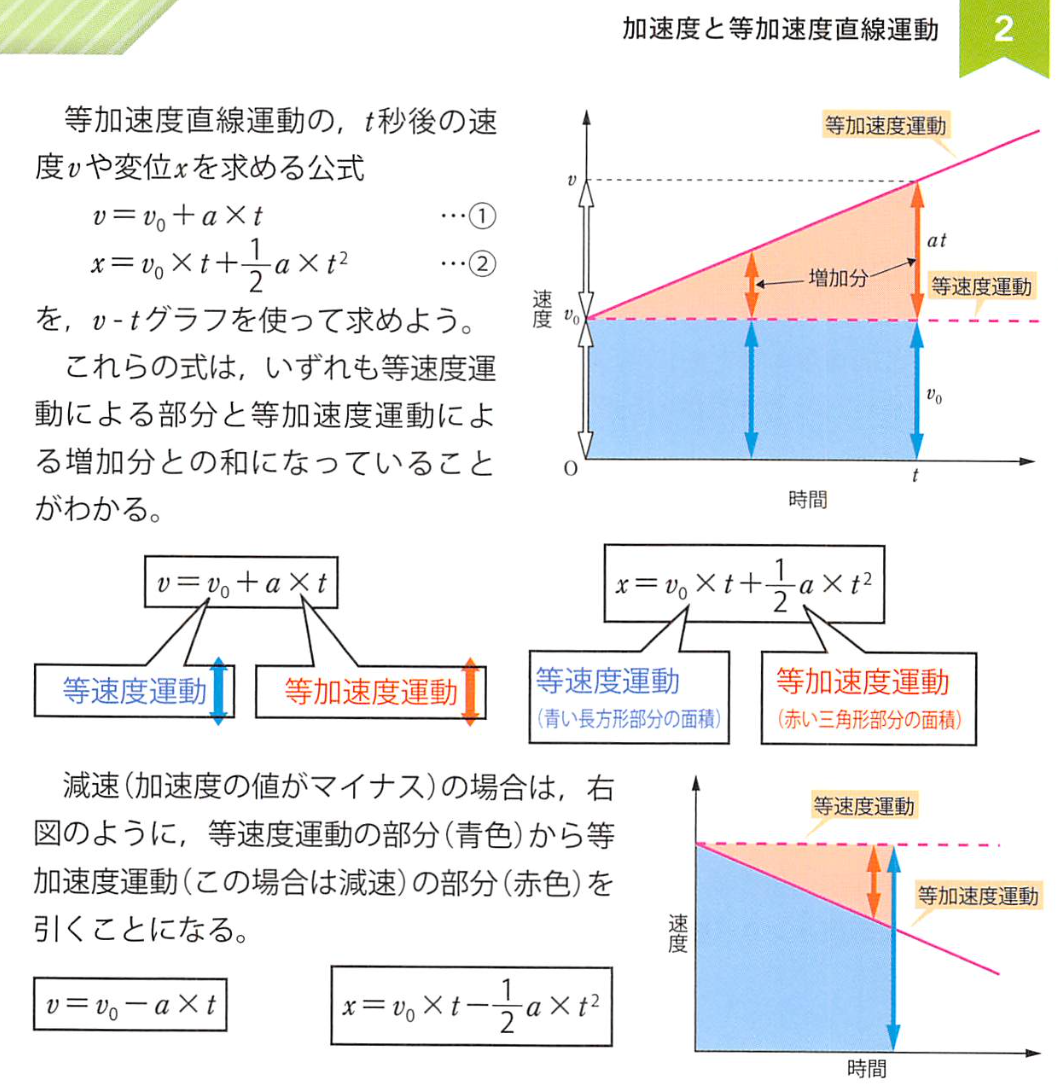
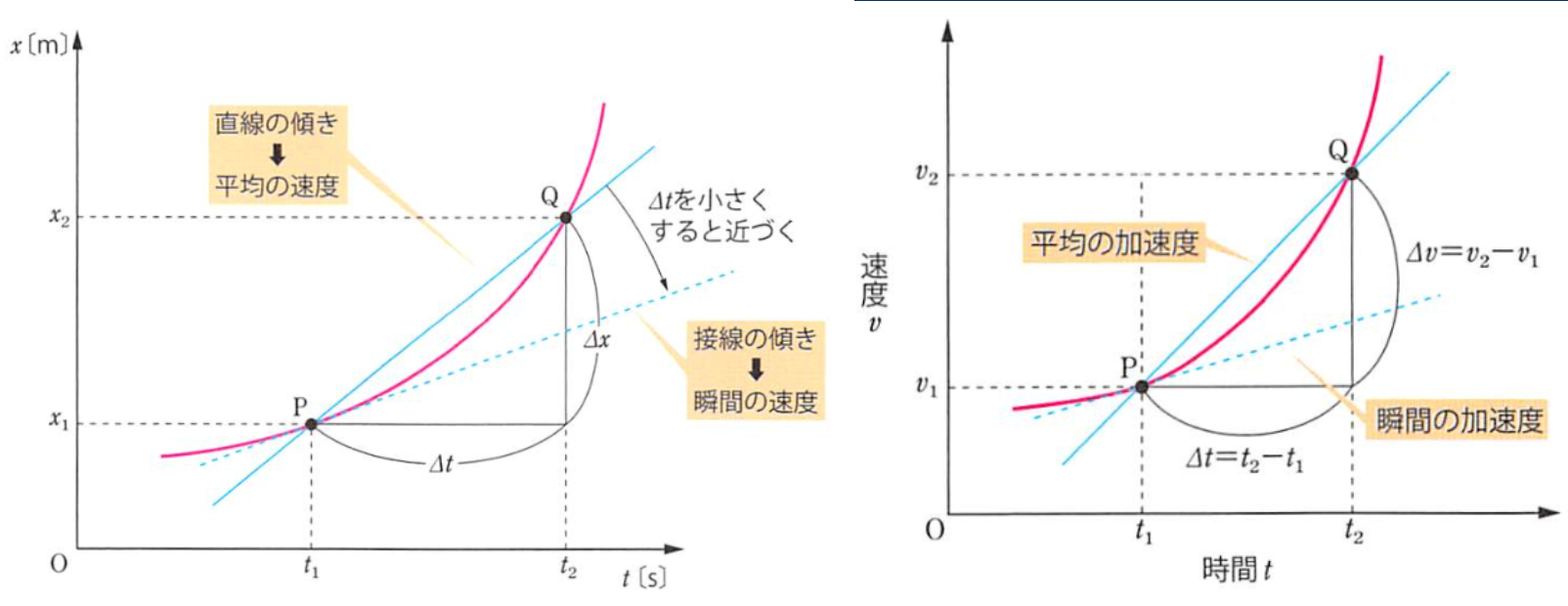
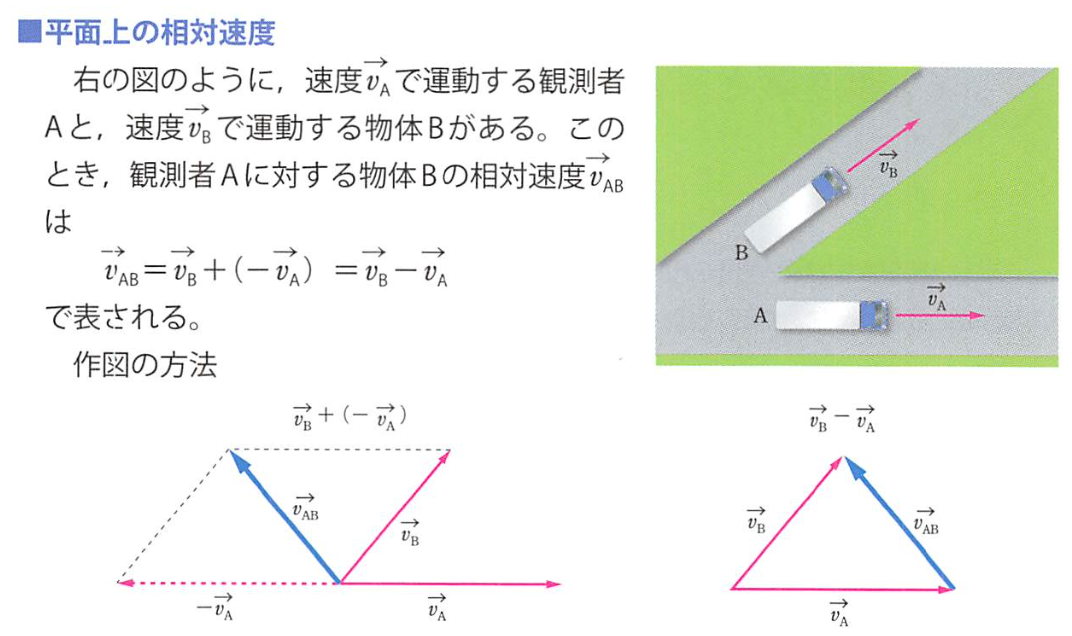
万有引力 gravitational force
万有引力定律 law of universal gravitation
波兰的哥白尼去世不久，丹麦的第谷·布拉赫诞生了，1560年14岁在看到了一次日食后便立志要从事天文学相关的工作。
$v=\omega r=\frac{2\pi rad}{24h}\times 6380km=464m/s=1670km/h$
第三宇宙速度（third cosmic velocity)是指在地球上发射的物体摆脱太阳引力束缚，飞出太阳系所需的最小初始速度。在地球轨道上要脱离太阳引力所需的初始速度为42.1公里/秒，但地球绕太阳公转时令地面所有物体已具有29.8公里/秒的初始速度，故此若沿地球公转方向发射，只需在脱离地球引力以外额外再加上适当的动能。
$\frac{1}{2}mv_3^2=\frac{1}{2}mv_2^2+\frac{1}{2}m(42.1-29.8)^2$
$v_3^2=11.2^2+12.3^2=16.7^2$
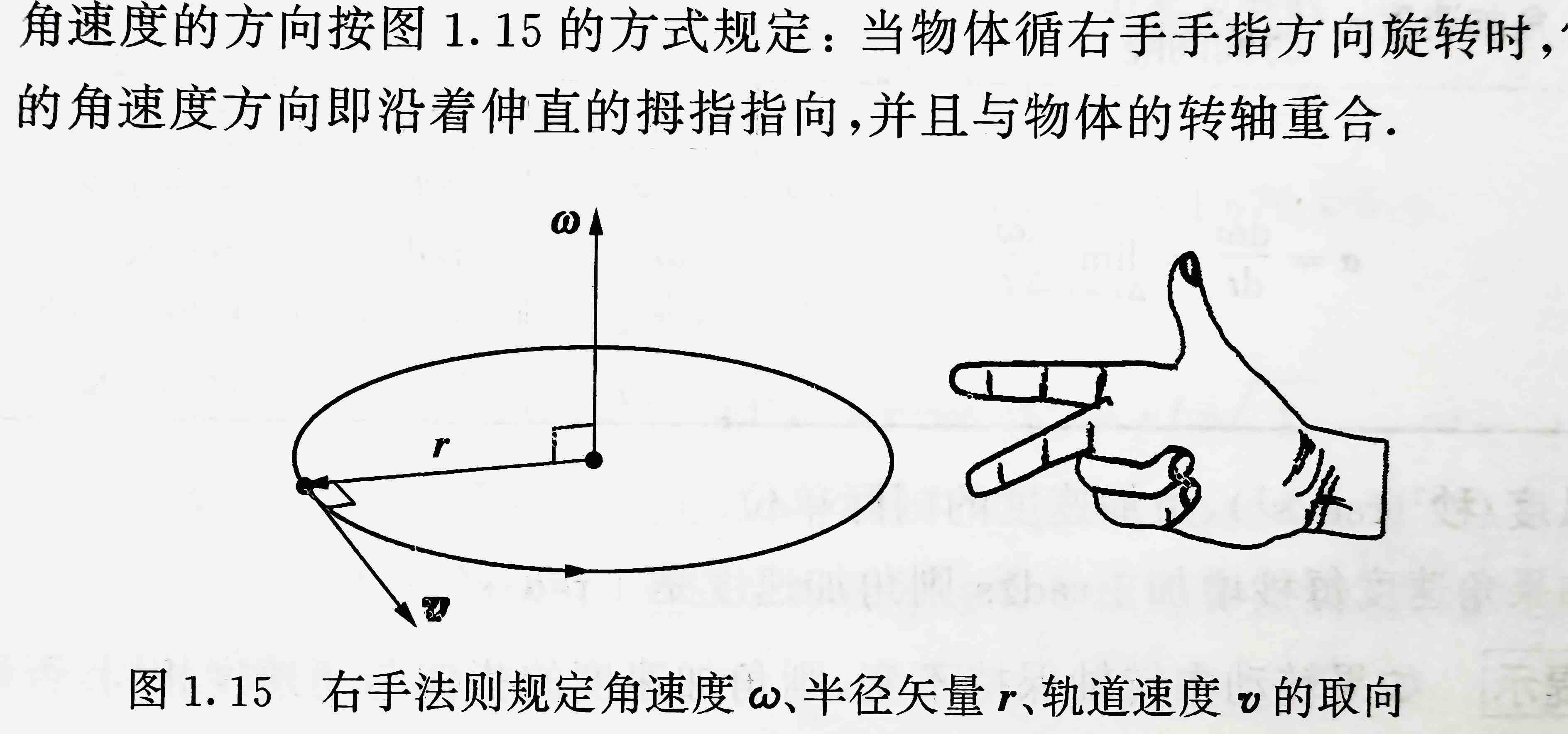
右手三指法则：角速度、半径矢量、轨道速度的方向分别沿着右手拇指、食指和中指的指向。

？第三宇宙速度：从太阳系逃生的速度
约30km/s。R从地球到太阳的距离1.496亿km做吧，M是太阳质量1.989×1030kg做。

第四宇宙速度：太阳系位置的银河系逃生速度
约300km/s。太阳系距离银河系中心约2.8万光年，怎么估计银河系的质量呢？

第五宇宙速度：从银河集团逃出的速度
约1000km/s。银河集团包括到哪个星系？

第六宇宙速度：从宇宙逃生速度
约30万km/s。好像只有光速才能逃脱。宇宙里本来就有“外面”吗？

$a=g(\frac{R}{R+h})^2$、$T=2\pi\sqrt\frac{r^3}{GM}$、$T=2\pi\sqrt\frac{R}{g}$
双星（甚至个别三星模型）$\frac{L^3}{T^2}=\frac{G(m_1+m_2)}{4\pi^2}$
两个相隔数百万千米的物体怎么会对彼此产生力的作用？爱因斯坦认为引力不是一种力，而是空间本身的一个种效应。是物体的质量改变了周围的空间，使空间弯曲，而其他物体则循着这种弯曲空间做加速运动。
引力场强度$g=\frac{F_g}{m}=\frac{GM}{r^2}$
惯性质量$\frac{F_n}{a}$
引力质量$\frac{r^2F_g}{GM}$
关于到底多少颗同步通信卫星能够完全实现全球通信的问题，多数回答三颗。这里谈的更具体一点[?]...

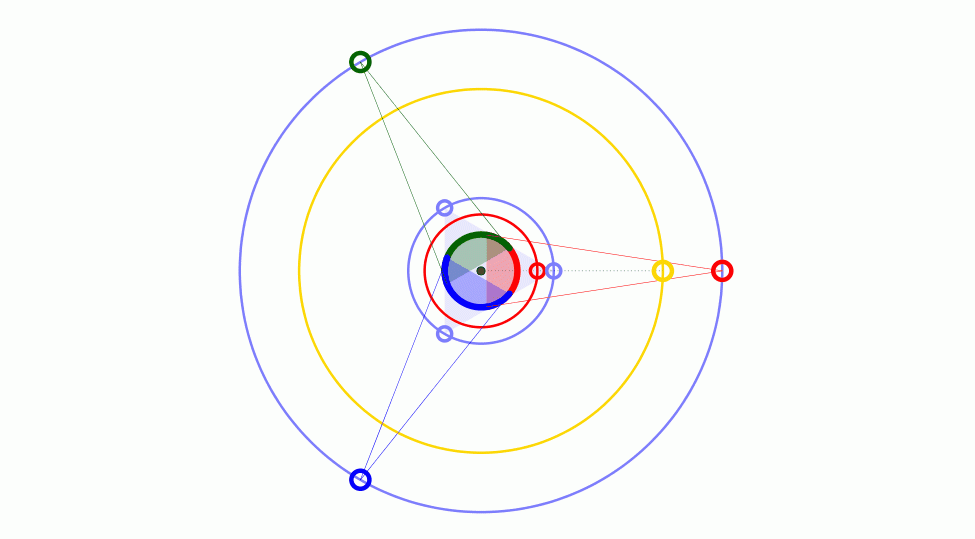
经典问题：
潮汐
拉格朗日点L3

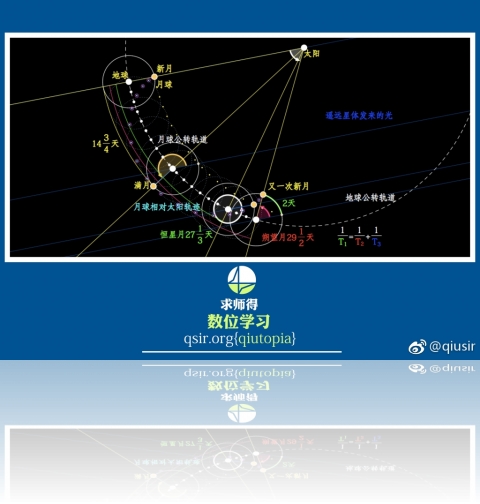
@qiusir:做了一个演示模型，关于月相周期（朔望月synodic，29天多）比月球公转周期（恒星月sidereal，27天多）多…… ​​​​
@qiusir:最近和学生讲万有引力定律的部分，找恒星月和朔望月资料时发现十几年前还算过一个有趣的结论：地球与月球极半径比约为3.66，和π/(4-π)非常近似，就说可以通过构造和地球外切正方形等周长的同心圆来近似构造出月球半径的相对大小。

今年全国II物理高考题（大多数题目算是简单到直接送分，审题和运算甚至高于物理知识的理解）的选择第7题不算简单，如果用我强调过的那个二级公式($\rho=\frac{3\pi}{GT_r^2}\frac{r^3}{R^3}$)要相对省事一些，另外一个也应该重视：$\rho=\frac{3\pi}{GT_0^2}\frac{g_0}{g_0-g}$，当然最简洁的还是$\rho=\frac{3\pi}{GT_1^2}$

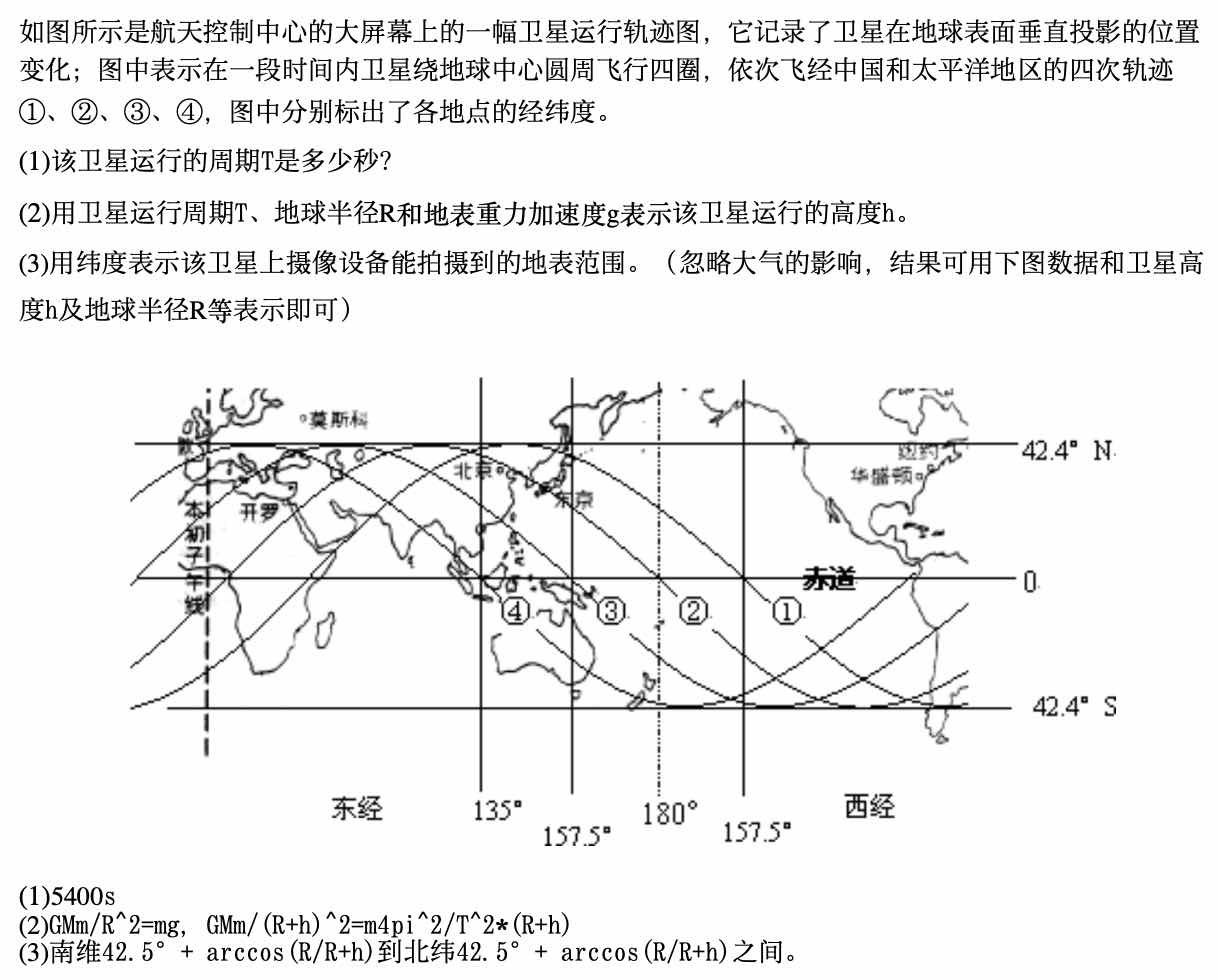
二模备选题，卫星平面图看周期以及高度和观测区间。

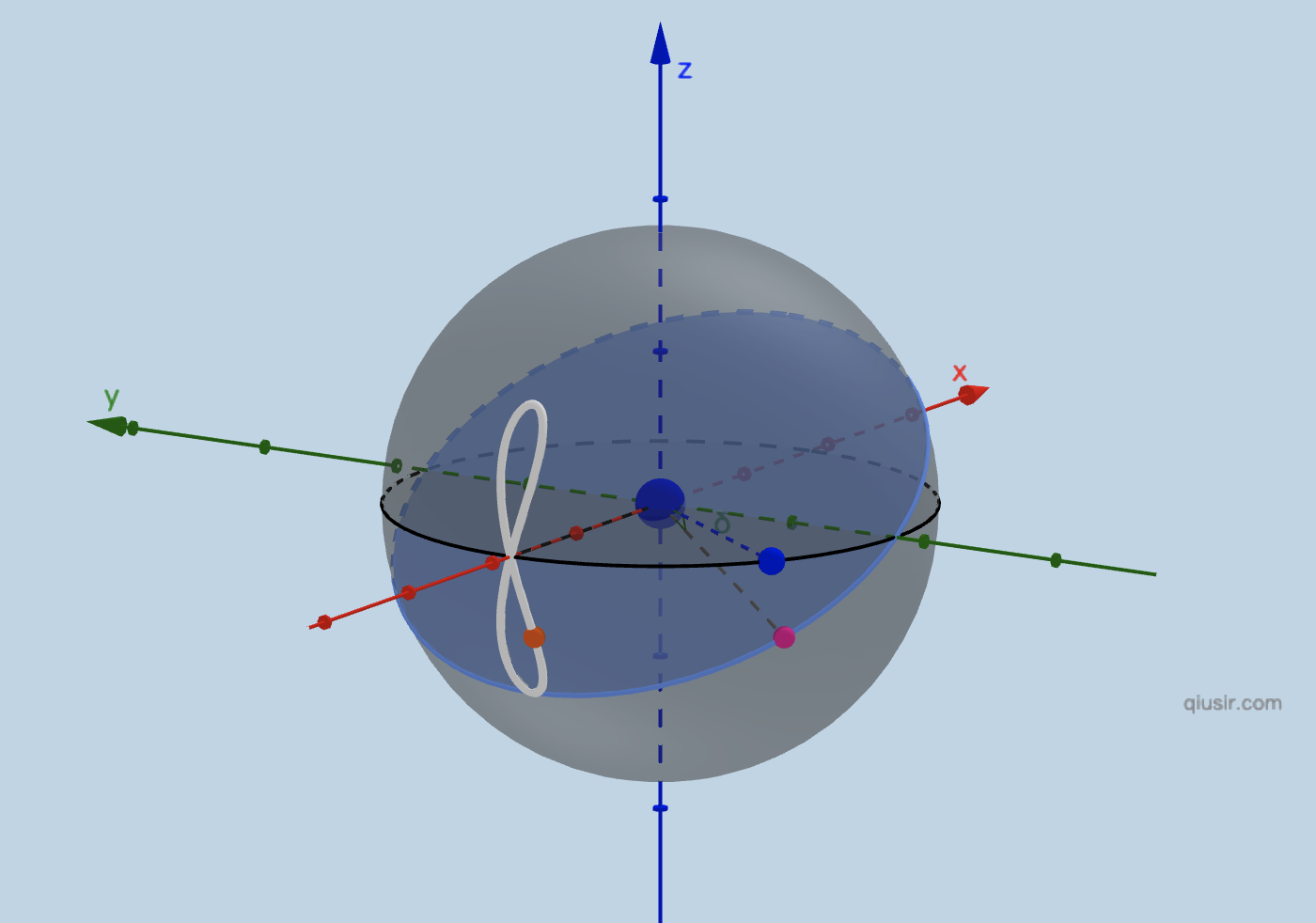
有学生对“地球同步倾斜轨道卫星相对于地面的运行轨迹”的问题很好奇，我抽空构造了简单的模型。要理解太阳的8字舞从这个问题开始会容易不少（有不少的地理知识需要补齐），除了日行迹（sun analemma，太阳在天球一年之中的行踪），当然也有月行迹(Analemma of the Moon)。

8-星行迹 [?]
人造重力[?

午间B班万有引力复习[?]

平面的匀速圆周运动$r(t)=\begin{pmatrix} rcos(\omega t)\\ rsin(\omega t)\\0\end{pmatrix}$，$v(t)=\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}$
$a(t)=\frac{d}{dt}\begin{pmatrix} -r\omega sin(\omega t)\\ r\omega cos(\omega t)\\0\end{pmatrix}=\begin{pmatrix} -r\omega^2 cos(\omega t)\\ -r\omega^2 sin(\omega t)\\0\end{pmatrix}=-r\omega^2 r(t)$
0、相对运动 $v_{ab}+v_{bc}=v_{ac}$
1、曲线运动
曲线运动一定是变速运动；曲线运动的物体一定受力；曲线运动可以是匀变速运动。
$\mathbf{a} =\mathbf{a}_{tan}+\mathbf{a}_{norm}=\frac{d(v\mathbf{e}_{tan} )}{dt}=\frac{dv}{dt}\mathbf{e}_{tan}+v\frac{d\mathbf{e}_{tan}}{dt}$
2、运动的合成与分解
交点的速度；同一根绳子／竿上的速度／角速度
渡船问题，如果船的速度小于河水的速度，如此情况下的航行的最小航程。
而沿某一方向可能有两个解。
3、探究平抛运动的规律
抛体projectile，拉丁文pro-向前，ject扔出去
（关于平等，地球对万物的力因为质量不同而不同，但都是具有相同的g，而特别的地区g也不同，这是一种平等的理解）
对匀变速运动物体相同时间间隔内位移增量等于aT^2要更熟练解决，还要对数字有更好的理解。
4、抛体运动的规律
位移和水平的夹角；速度和水平的夹角；相当于从中点发出的。
射程的问题；最高点竖直速度为零。

匀变速曲线运动平均速度$\frac{x}{t}$、$\Delta x=aT^2$的向量性以及和中间时刻瞬时速度等可以从匀变速直线运动迁移过来。
(eg:t=1\3\5经过(0,0)(8,0)(8,6)加速度2.5)

斜抛运动坐标系变换看运动合成。（斜的匀速直线运动和自由落体的叠加）
$L=v_0t$
$x=v_0cos\alpha t=L cos\alpha$
$y=v_0sin\alpha t-\frac{1}{2}gt^2=L sin\alpha-\frac{1}{2}gt^2$
5、圆周运动
$\frac{\Delta r}{r}=\frac{\Delta v}{v}$
两边同除以$\Delta t$
$\frac{\Delta r}{r\Delta t}=\frac{\Delta v}{v\Delta t}$，$\frac{v}{r}=\frac{a}{v}$
6、向心加速度
通过速度的水平和竖直分量的导数，求解出水平和竖直的加速度，求解合加速度。
7、向心力
8、生活中的圆周运动
公路在通过水库泄洪闸下游时常常要修建凹形桥，也叫过水路面。

勾股定理求位移大小后通过平均速度求$v_A$
·一道运动学题目的多种解法[?]
·等速圆周的向心力证明[?]

运动学 静力学 动力学
惯性质量：表示物体对改变它的运动状态的阻抗性。
1、牛顿第一定律
Pope:Nature and nature's law lay hid in night. God said,let Newton be! And all was light.
1687年，牛顿出版《自然哲学的数学原理》
牛顿第一定律是利用逻辑思维对事物分析的产物，不可能用实验直接验证。

2、探究加速度与力、质量的关系
控制变量的方法，m,F
化曲为直的思路。
平衡摩擦力的尺度，小筒质量过大，线段平移弯曲等分析。

3、牛顿第二定律

4、力学单位制
质量，时间，长度。电学是安培。

5、牛顿第三定律
作用力与反作用力一定是同一种性质的力，而平衡力未必。
作用力反作用力的功各种情况都可以。
而摩擦力的功要特殊一些。
6、用牛顿定律解决问题

当物体处于动态平衡时，作用力之和力与静止系中惯性力之和为零。
倾角α的正切值是高度差与水平位移之比，称为梯度。

引力质量与惯性质量相等时被实验证实了的事实，也是广义相对论的出发点。

GHT同学推荐题目：

因为$a^2+b^2=c^2$，所以3±4=5

1、重力 基本相互作用
重力和万有引力的关系

2、弹力
自然界的四种基本作用力是不需要接触就能起作用的。
弹簧剪短，串联并联，劲度系数.Hooke law
3、摩擦力
$F_{f,s}\le \mu_sF_N$
4、力的合成
(F1+F2)^2
三角形法则。
5、力的分解
6、平衡

光滑碗里细线的两个球的受力，战鸽同学的矢量三角形的方法。

日语教材上的分类
▼接触力の例
　張力(Tension)　T
　垂直抗力(Normal Reaction)　N
　摩擦力(Friction)　f
　弾性力　kx

▼遠隔力の例
　重力　mg
　静電気力　qE
　磁力
　核力

[鉛直方向]Tsin30°=W
Hookeの法則（法则一说来自日语啊？）
Atwoodの器械

$\frac{1}{2}mv^2$

滚动摩擦$F_r=\frac{f}{r}F_N$滚动摩擦系数f（量纲是长度）表达了支持力$F_N$与摩擦力矩M之间的比例关系。$M=r\cdot F_r=fF_N$

一道立体模型的摩擦力题

http://www.qiusir.com/?p=19609

斜面置物

http://www.qiusir.com/?p=1799

via[?]
一般性的匀变速运动中间时刻的位置与运行中点位置间的距离公式$\frac{1}{8}aT^2$（四种方法，代数法、中间时刻和中点速度公式、图像割补以及等分苹果$\frac{1}{2}a(\frac{T}{2})^2$）

p36纸带法绘制v-t图像。
导数和积分的问题可以结合到a v s 上。
p44光电门的应用。
光电门测加速度误差分析。测量值大于真实值
$a=\frac{(\frac{d}{\Delta t_1})^2+(\frac{d}{\Delta t_2})^2}{2L}$
频闪摄影

相对速度比速度合成更生活化。

a accelerationの頭文字

（公式增加动能变为一半（前后两个过程合外力的功一样）和动量变为一半（前后合外力的冲量一样））
（孙浚豪整理）运动学公式整理：

·基本公式：
$\bar{v} =\frac{x}{t}$
$v=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}$
$v={x}' \left ( t \right )$
$a=\lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t}$
$a={v}' \left ( t \right ) ={x}'' \left ( t \right )$
$v=v_{0}+at$
$x=v_{0}\cdot t+\frac{1}{2} at^{2}$
$x=v_{t}\cdot t-\frac{1}{2}at^{2}$
$x=\bar{v}\cdot t=\frac{v_{0}+v_{t}}{2} t$
$v_{t}^{2}-v_{0}^{2}=2ax$
$\bar{v}=v_{\frac{t}{2}}$
$\bar{v}=\frac{v_{0}+v_{t}}{2}$
$v_{\frac{x}{2}}=\sqrt{\frac{v_{0}^{2}+v_{t}^{2}}{2} }$
两个连续时间间隔T的位移差：$\Delta x=aT^{2}$
第n个T与第m个T的位移差：
$x_{n}-x_{m}=\left ( n-m \right )aT^{2}$

·初速度为0的匀加速直线运动：
前T时间内中间时刻位置与中间位移的距离：$d=\frac{1}{8}aT^{2}$
$T,2T,3T\dots \,nT$ 时间末物体瞬时速度之比：
$v_{1T}:v_{2T}:v_{3T}: \cdots :v_{nT}=1:2:3:\cdots :n$
$T,2T,3T\dots \,nT$ 时间内物体平均速度之比：
$\bar{v}_{1T}:\bar{v}_{2T}:\bar{v}_{3T}:\cdots :\bar{v}_{nT}=1:2:3:\cdots :n$
$T,2T,3T\dots \,nT$ 时间内物体位移之比：
$x_{1T}:x_{2T}:x_{3T}: \cdots :x_{nT}=1:4:9:\cdots :n^{2}$
物体通过$x,2x,3x\dots \,nx$ 位移末瞬时速度之比：
$v_{1x}:v_{2x}:v_{3x}: \cdots :v_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体通过$x,2x,3x\dots \,nx$ 位移所需时间之比：
$t_{1x}:t_{2x}:t_{3x}: \cdots :t_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体通过$x,2x,3x\dots \,nx$ 位移过程平均速度之比：
$\bar{v}_{1x}:\bar{v}_{2x}:\bar{v}_{3x}: \cdots :\bar{v}_{nx}=1:\sqrt{2} :\sqrt{3}:\cdots :\sqrt{n}$
物体经过连续相等时间内位移之比：
$x_{T_{1}}:x_{T_{2}}:x_{T_{3}}: \cdots :x_{T_{n}}=1:3:5:\cdots :\left ( 2n-1\right )$
物体通过连续相等位移所需时间之比：
$t_{x_{1}}:t_{x_{2}}:t_{x_{3}}:\cdots:t_{x_{n}}=1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):\cdots :(\sqrt{n}-\sqrt{n-1})$
静止开始，物体通过连续相等位移平均速度之比：
$1:\sqrt{2}+1:\sqrt{3}+\sqrt{2}...\sqrt{n}+\sqrt{n-1}$
$x_n=v_0T-\frac{1}{2}aT^2+naT^2$

$v(t)=\sqrt{v_0^2+2ax(t)}+v_0$

$x(t)=\frac{v(t)-v_0}{2}t+v_0t+x_0$（从梯形面积的角度考虑）
另，为了更好理解$\Delta x=aT^2$，特别进行了表格训练（匀变速运动）...

[?]一道运动学题目的多种解法