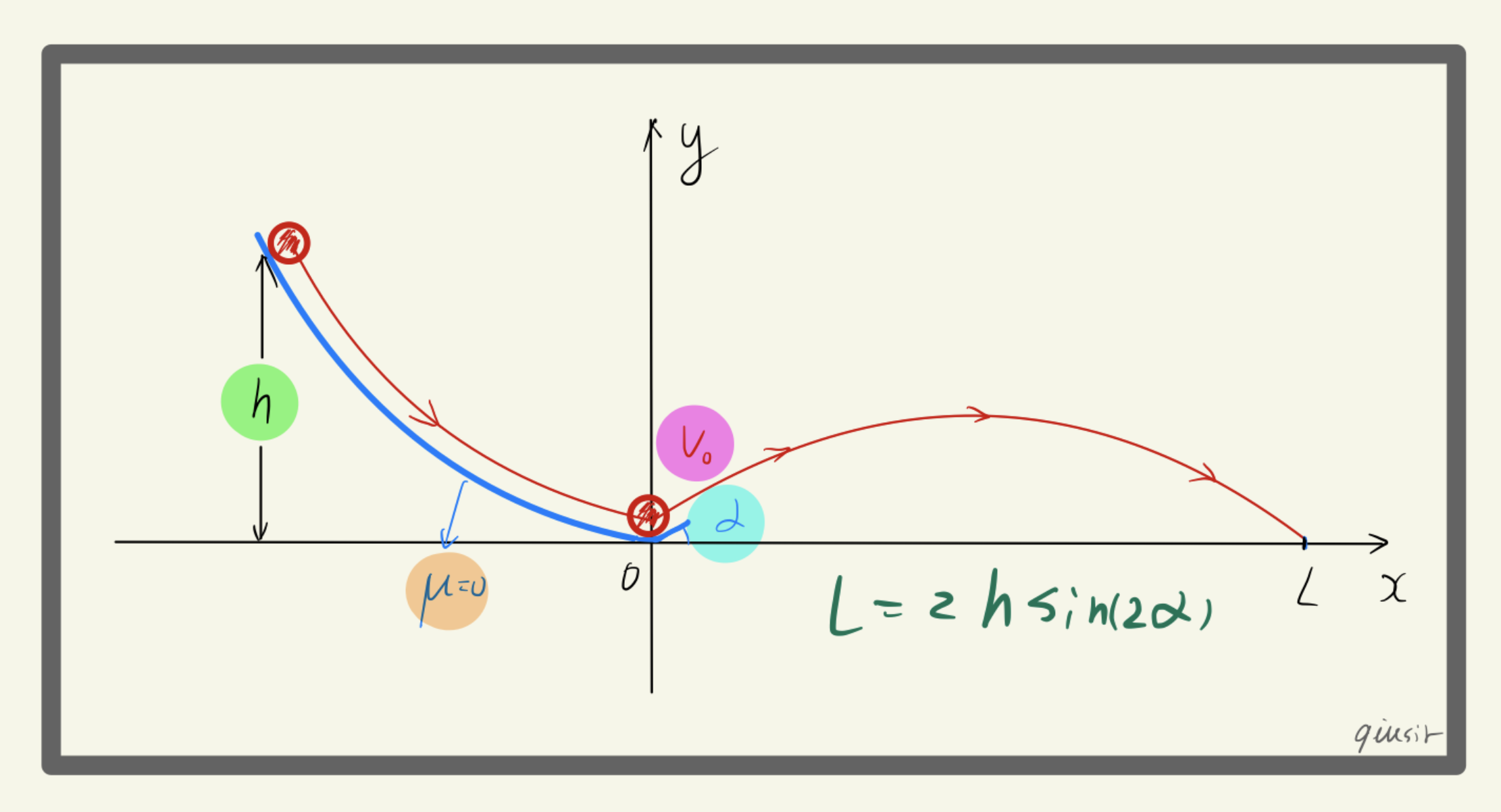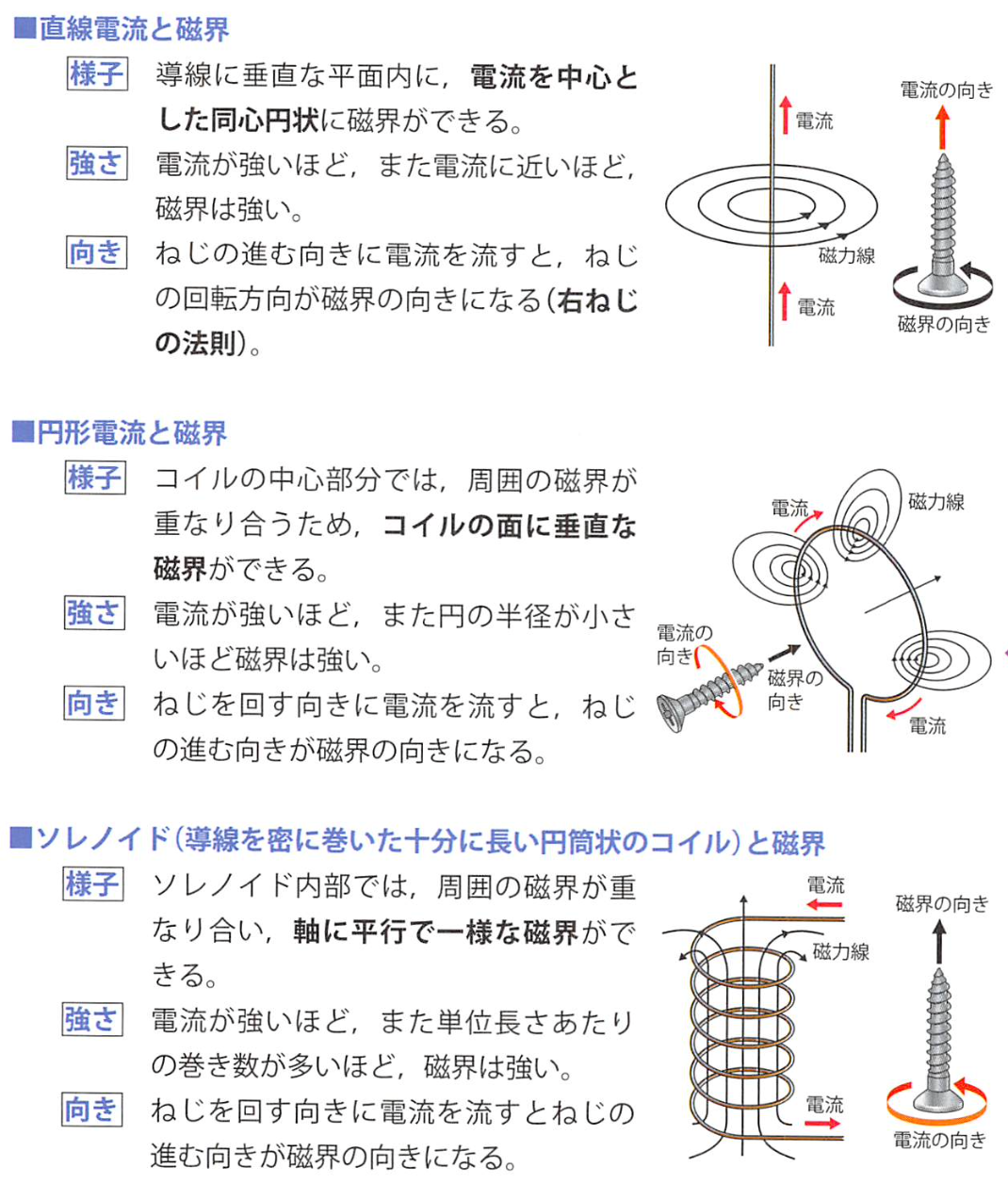
配速法总结
重力(或电场力)的功率等问题
理论上,


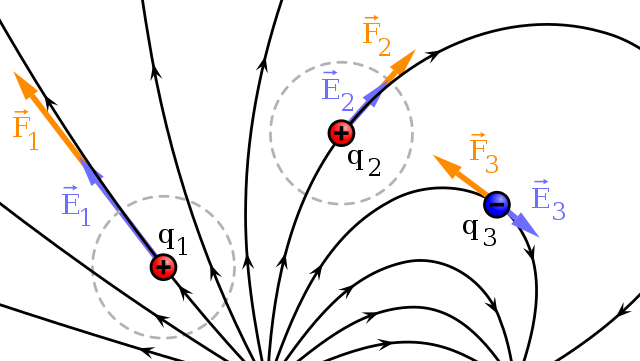


https://tikz.net/electric_fieldlines2/
关于电场的理解,翰铮从B站上看到“臭脚丫”的例子...
后来我觉得用榴莲比喻可能更好,有的人喜欢榴莲有的人很反感榴莲...
http://www.qiusir.com/?p=27438
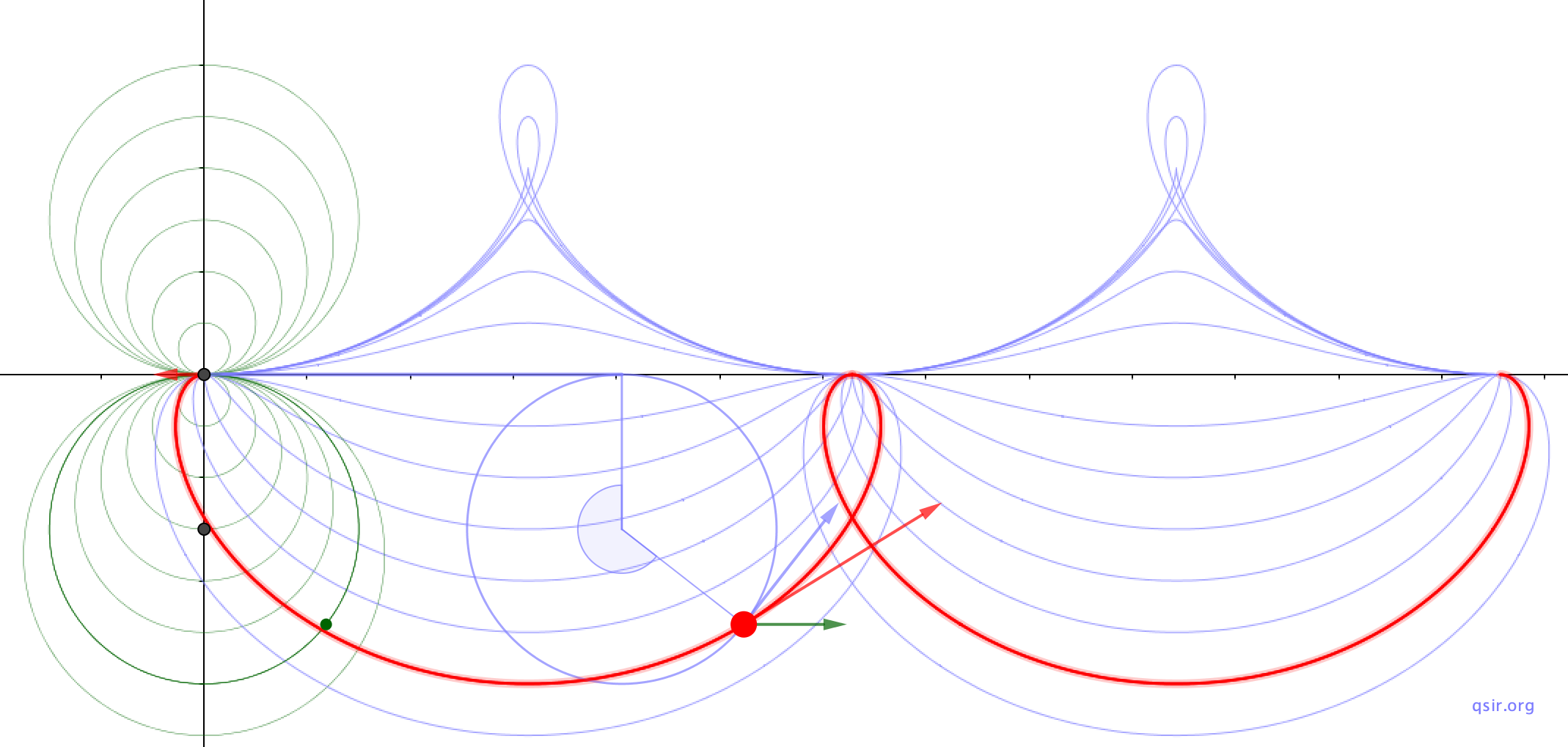
电场线方程
https://zhuanlan.zhihu.com/p/150129957
https://zhuanlan.zhihu.com/p/148638744
网课的习题备份。动能定理,类平抛,竖直面圆周运动,等效重力场,速度分解,绳导致能量损失...
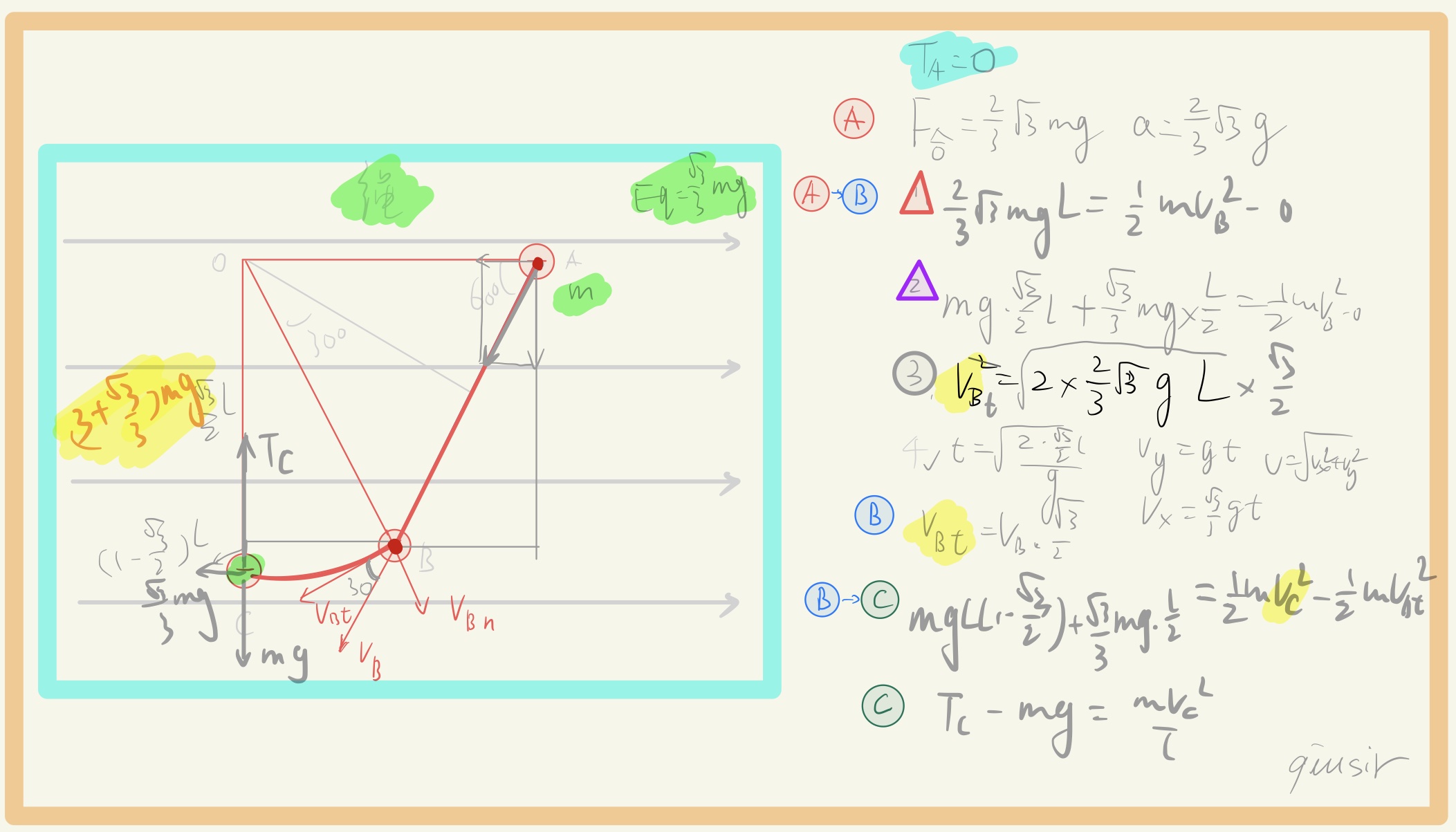
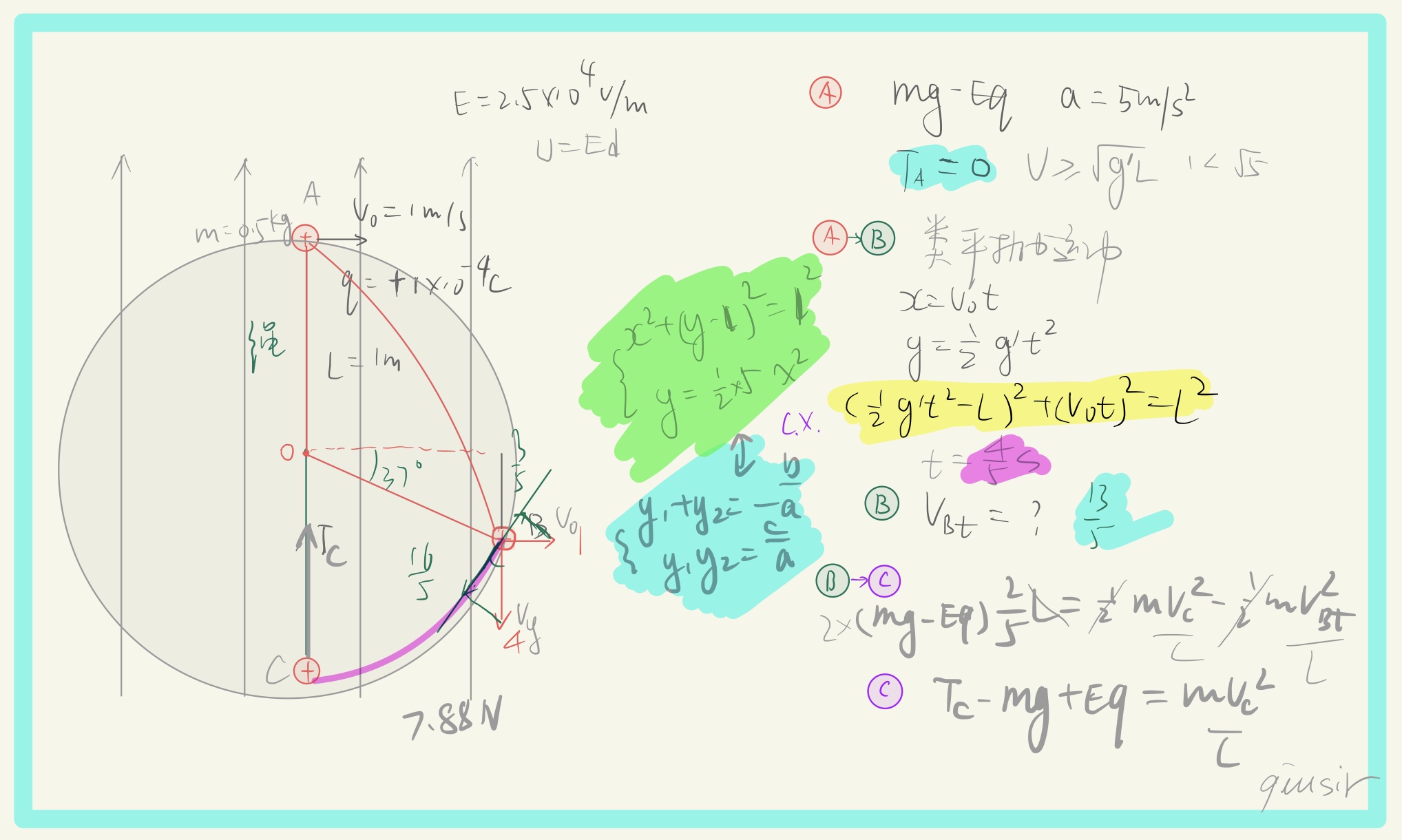
等量异种带电圆环的电场强度和电势的变化图像。
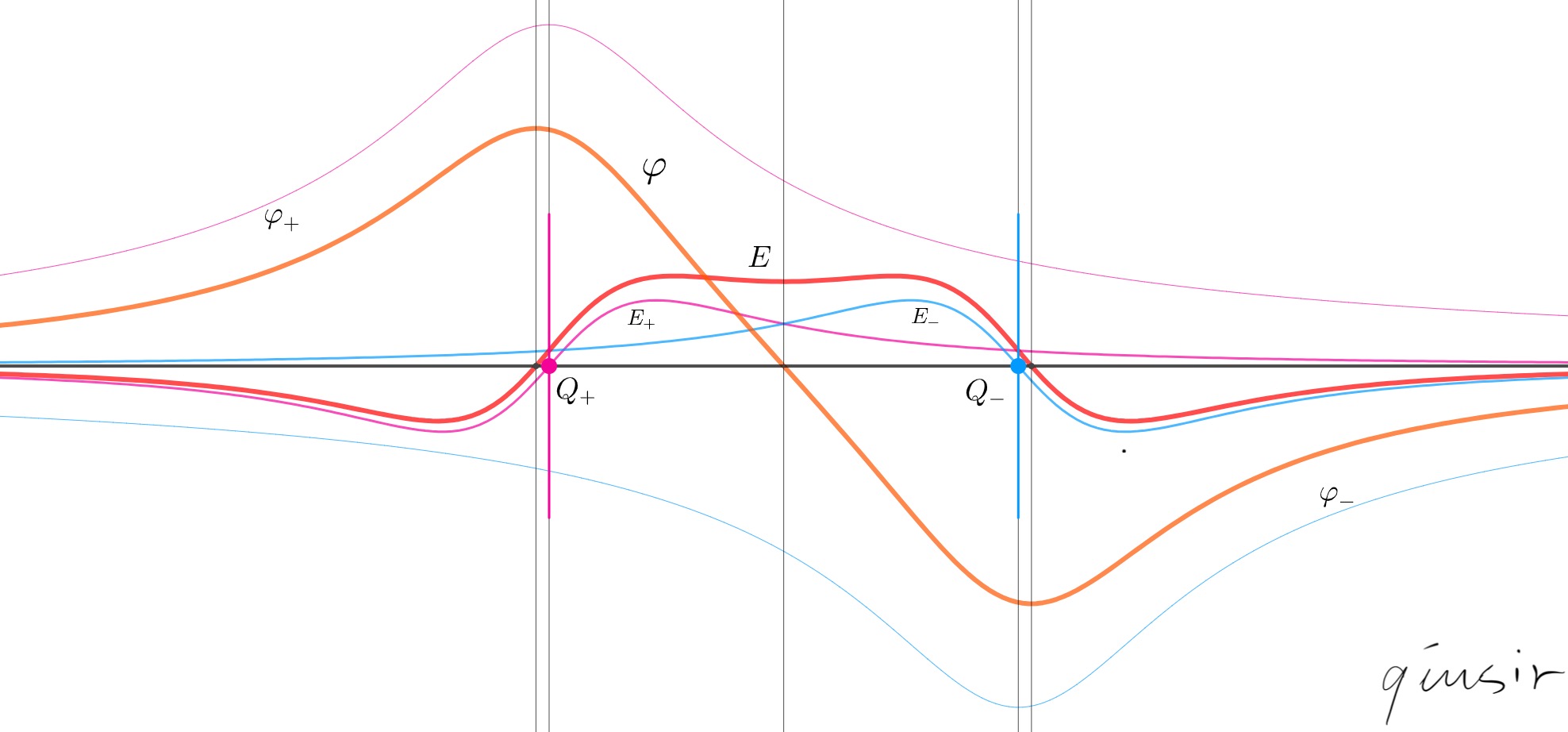

 取等
取等
对于直径上q和8q电荷,另一同种电荷在光滑半圆上的动能极大或稳定点,也是电势能最小的位置,除了用电场强度的方向是圆心方向,可以继续用权方和不等式,而不需要对电势求导求。
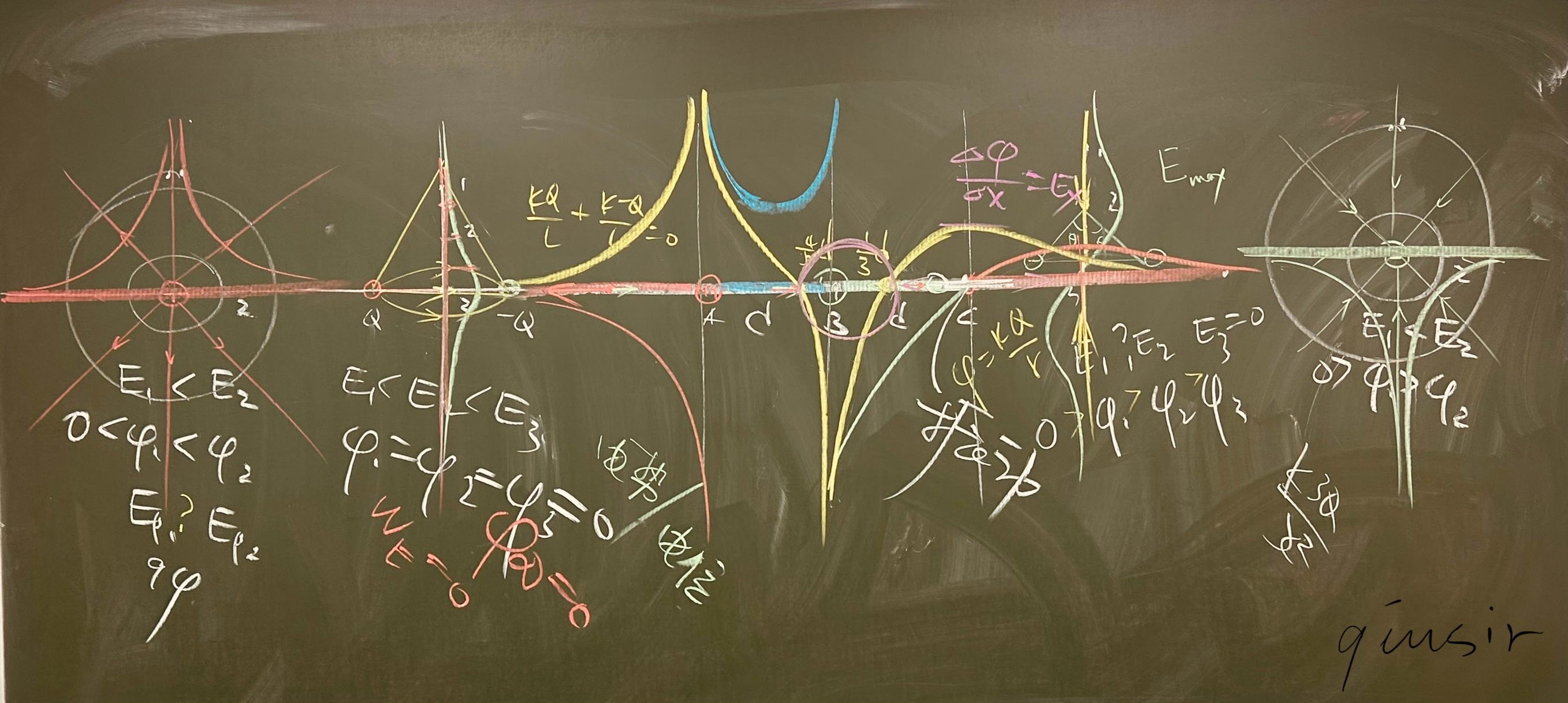
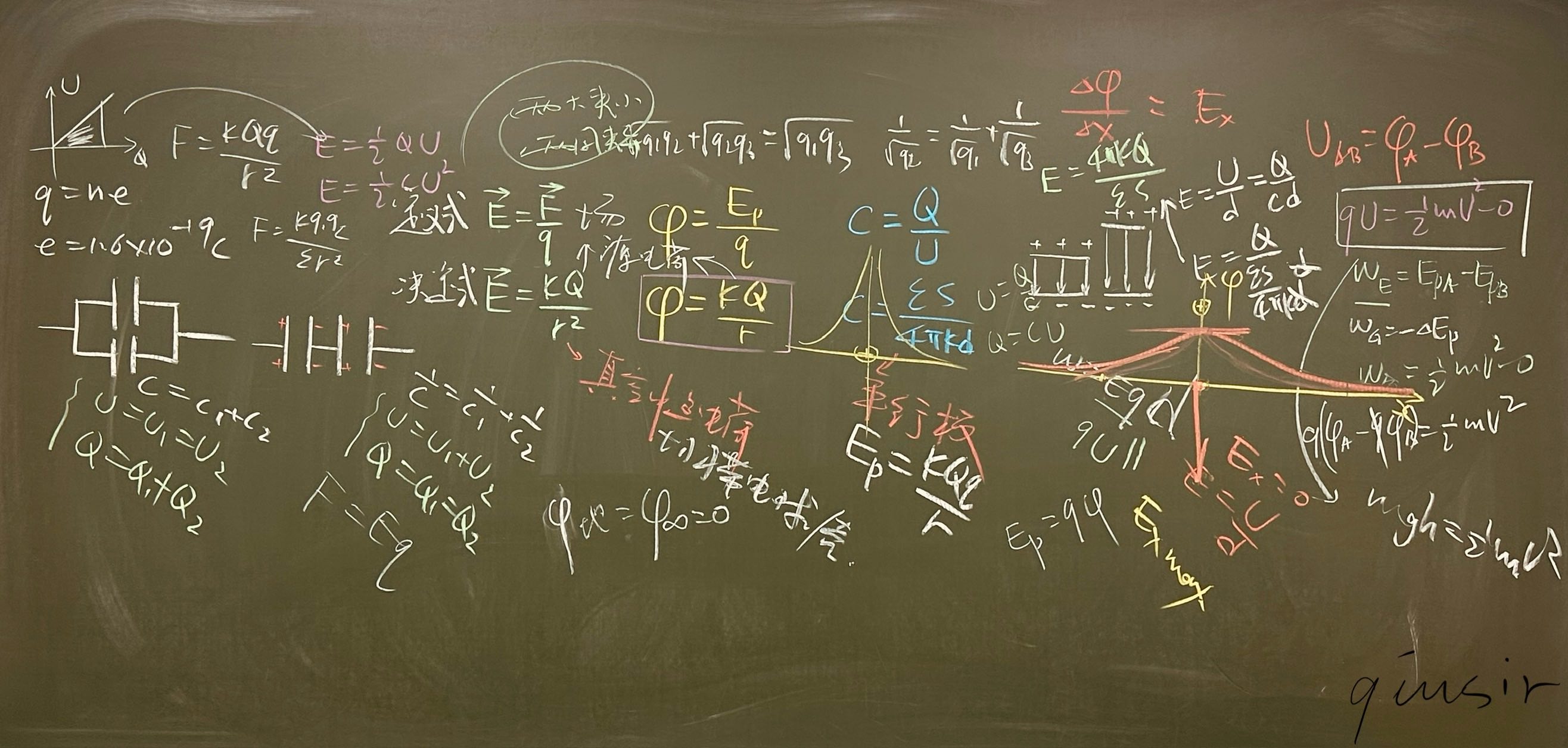
常见问题
库伦用扭称测得静电力常数×
接地的物体不带电×
静电器是一个小电容√
电容串联电量等、并联电压等√
想象远比知识重要,知识有涯,而想象能环保整个世界。(逻辑带你从A点到B点,想象带你到任何地方。)---爱因斯坦
1、探究碰撞中的不变量
注重实验的引入,注意弹性碰撞动能守恒的特例。
2-3、动量守恒
动量守恒认知的历史过程。笛卡尔最初提出,但他忽略了动量的方向性,后来的惠更斯给出动量守恒的最初表述。牛顿明确用质量与速度乘积来定义了动量。
利用牛顿第三定律和第二定律推导动量守恒。
动量守恒不仅是始末两个状态,而是整个过程一直保持不变。我们才说这个过程动量守恒。
实验证明,高速微观领域,牛顿定律不再适用,但动量守恒依然正确。
电磁波也具有动量,它与粒子的相互作用也遵守动量守恒定律。
动量守恒是一个独立的实验定律,它适用于目前为止物理学研究的一切领域。
4、碰撞
对心碰撞,弹性碰撞,非弹性碰撞,完全非弹性碰撞(损失动能最大,相当于中间弹簧的型变量最大,弹性势能储存最多)
代数法推导。
图像法,共速时,弹簧压缩最大或者是拉伸最大,弹性势能最大,动能损失最多。
特殊情况的讨论。对交换速度的解释。

王聪和万炳文两位同学对v-t图像与动量问题的解决方面提供了很好的办法。[?]
对于弹性碰撞模型的解决,等效弹簧,人船模型,相对速度的问题,都有很好的帮助。
以学教学,再发现

角动量是与物体的位置向量和动量相关的物理量。对于某惯性参考系的远点, ,
, ,
,
当物体的运动状态(动量)发生变化,则表示物体受力,而作用力的大小等于动量的变化率。 (直线运动中,F=ma)(一般物体的动能
(直线运动中,F=ma)(一般物体的动能 )
)
当物体的转动状态发生变化时,则表示物体受到力矩作用,而力矩就等于角动量的变化率(时变率) (旋转运动中,
(旋转运动中, )(转动动能
)(转动动能 )
)
静电力或万有引力均是径向力,因此不会产生力矩。行星运动满足角动量守恒,对应的就是开普勒定律中的第二定律。
动量表示物体达到目前运动状态所获得的全部力的冲量之总和。只有受到力的作用时,这些储存的冲量才会释放出来。
合力 resultant force
质心坐标
质心速度求解,日本教材上
http://www.qiusir.com/?p=31451
相对质心的速度等效人船模型。



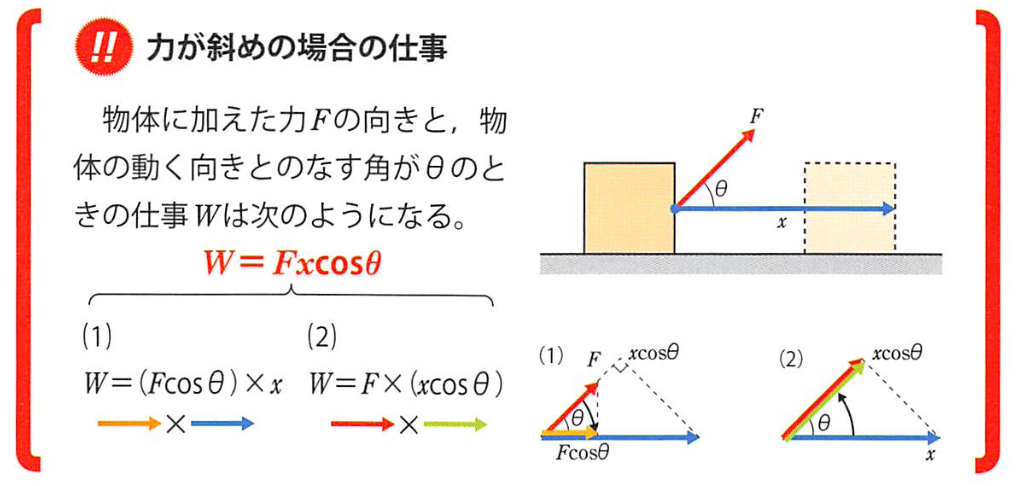
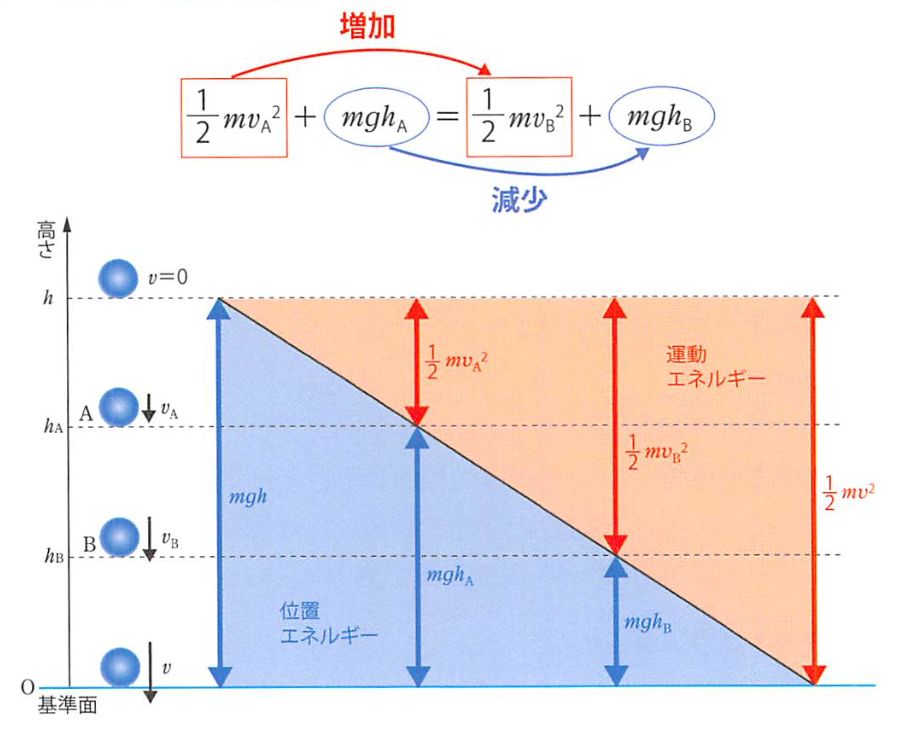
加速过程中做的功,克服以加速度a加速的质量m的惯性力ma所做的功。 由于加速过程中功仅仅与始末速度有关,对于力随时间而变的情况,
由于加速过程中功仅仅与始末速度有关,对于力随时间而变的情况, 也能成立。(物体滑上传送带上产生的热量也是这个公式?)
也能成立。(物体滑上传送带上产生的热量也是这个公式?)