五 03

李海妹 Lauralee
东北育才学校高级教师、求师得数位学习联合创办人、《数字故事讲述》课程主持人
全国创新英语大赛总冠军特级辅导教师、全国中小学生英语大赛团体赛全国总冠军指导教师、沈阳市名师进课堂讲师团成员...
读后续写写作攻略
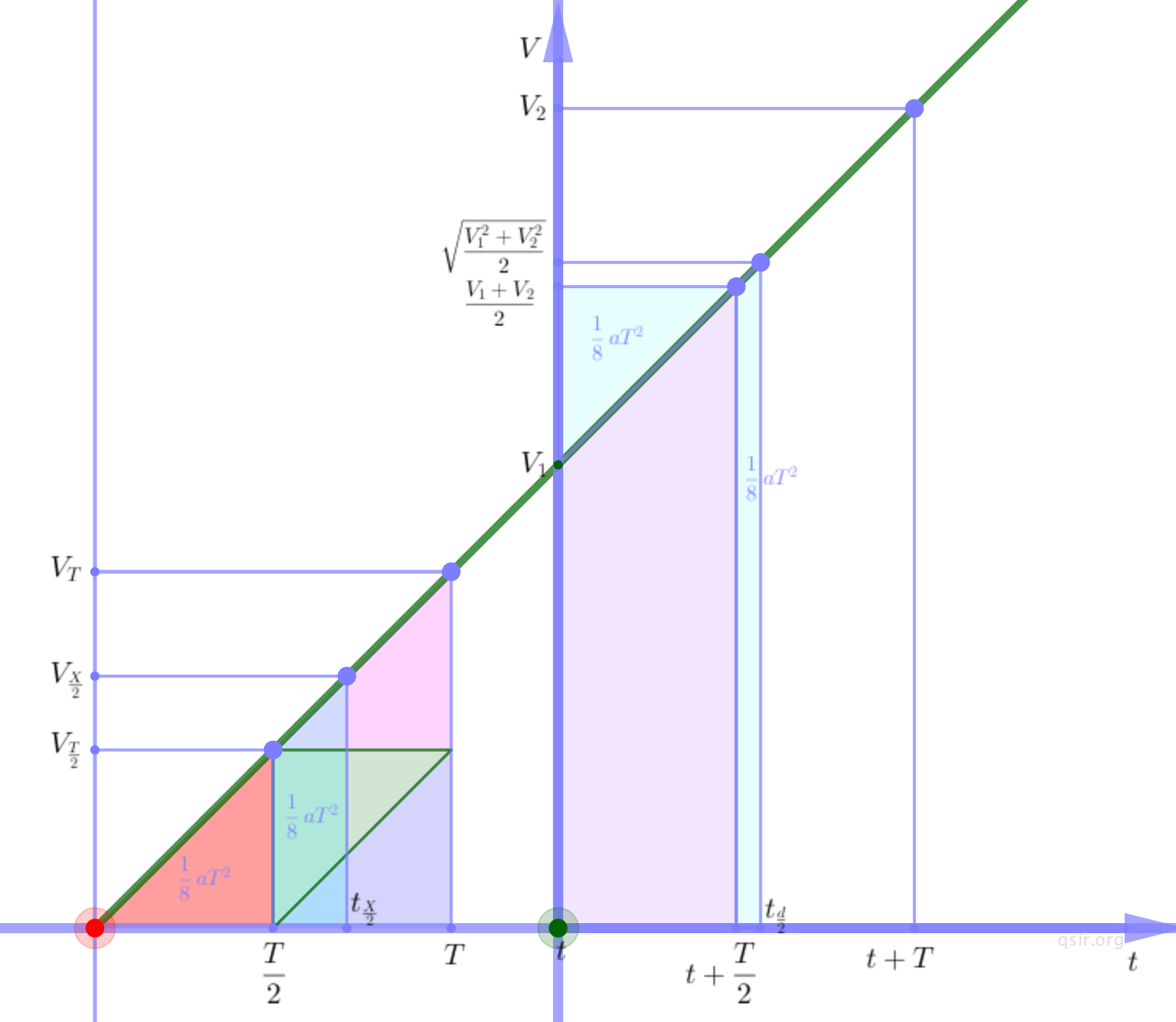
读后续写中读的过程要做到找、划、猜。找文章的主题,划出表现人物性格/推动情节发展的词句,猜测故事的内容走向。
下面我们以沈阳市二模为例演示写作过程。
1.找主题 Theme: kindness from strangers
2.编内容
Para 1 接到电话后担心紧张;打手机询问打不通;决定转钱
Para 2 紧张被店员注意;店员报警真相大白;感激/升华
3.分配细节
Para 1 担心紧张的心理/表情描写;决定转钱时的连动
Para 2 两人对话的语言描写 ;得知真相后的心理描写
4.写草稿
Para 1 Cecil was totally at a loss. Astonished and suspicious, he called David's mobile phone to see what happened. However, the line was busy, which made him more anxious. Worrying about his grandson, he found his credit card and set off for Walmart.
Para 2 The lucky part of Cecil's day was when he stepped into cashier Audrella's line in Wal-Mart. "How can I help you?" she asked gently. "I need to transfer $2300 to another store."said Cecil nervously. Sensing his nervousness, Audrella asked if everything was okay. After Cecil told her the whole story, Audrella called the police. When two officers arrived, Cecil were calm again and realized that the whole thing was a phone scam. Cecil held Audrella's hands, and thanked her sincerely for her kindness and love.
5.语言润色
Para 1 Cecil was totally at a loss. With a mixture of astonishment and suspicion, he called David's mobile phone, attempting to figure out what on earth had happened. However, after calling up to 10 times, the line was busy all along, which only added to his anxiety all the more. Worrying about his grandson, feeling no time to waste, he took his credit card, started the car and off he went.
Para 2 The lucky part of Cecil's day was when he stepped into cashier Audrella's line in Wal-Mart. "How can I help you?" she asked gently. "I...I need to transfer $2300 to...to another...store." stammered Cecil, sweat rolling down his forehead. Sensing his nervousness, Audrella couldn't help asking if everything was okay. With a shaking voice and reddened eyes, Cecil told her the whole story, pinning all his hopes on this young girl he'd never met before. Burning with mounting suspicion, Audrella called the police. With the arrival of two officers, Cecil regained his calm and came to the realization that the whole thing turned out to be nothing but a phone scam. Holding Audrella's hands tightly, Cecil couldn't thank her enough and gave her $100 in reward, knowing too well that no price was too high for the random act of kindness and love.
Continue reading »
四 19

物理笔记PDF文件下载:
PHY-1804日语班贾钟哲物理笔记 (2500)
恭喜贾钟哲同学!东京大学工学部物理工学科!!!from J.Kevin @20220319
·[?]优秀学长说“求师得优秀物理笔记荣誉”...
三 29

还在读初二的孙浚豪同学已经可以解决那道典型的动力学问题,他一整天除了吃放基本都在运算,还用电脑精确完成了速度时间图像的绘制,我通常用说这道题目可以判断学生是否有资质去搞物理竞赛,当然这道题目通过动能定理或是功能关系会很容易...
Continue reading »
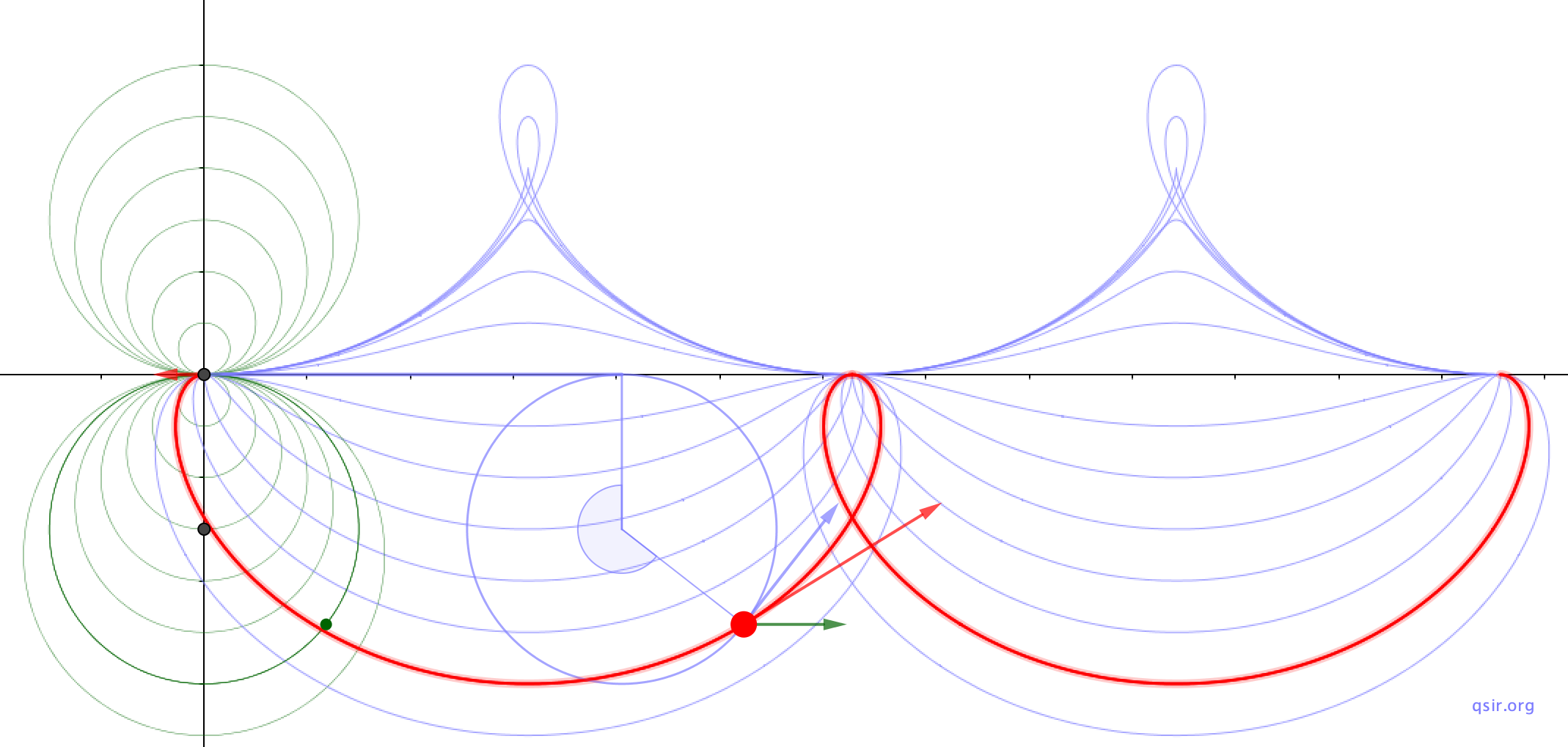
 和能获得最大速度
和能获得最大速度 ...
... 一定是水平的(
一定是水平的( )。根据动能定理和水平方向动量定理,可得:
)。根据动能定理和水平方向动量定理,可得:




 ,主要的意图是水平向右的速度对应的洛伦兹力能平衡掉重力,这样,带电小球的运动就可以转化为逆时针圆周运动与水平向右匀速直线运动的合成,轨迹是摆线。
,主要的意图是水平向右的速度对应的洛伦兹力能平衡掉重力,这样,带电小球的运动就可以转化为逆时针圆周运动与水平向右匀速直线运动的合成,轨迹是摆线。 ,而下落最大高度
,而下落最大高度
 ,得
,得 ...
... ,
, ,再比如,如果小球的初速度是倾斜的,通过上图应该可以想到,运动的轨迹是水平的
,再比如,如果小球的初速度是倾斜的,通过上图应该可以想到,运动的轨迹是水平的 和小球初速度与
和小球初速度与 矢量差为线速度的圆周的叠加,当然回过头看,前面的讨论不过此前提下的是特例。
矢量差为线速度的圆周的叠加,当然回过头看,前面的讨论不过此前提下的是特例。