JQX/进取芯 小教研第四期(2025.4.16)

关于周期:
Qiusir以学生随意发挥(意识流)的形式带领学生(新疆部)总结高中很多关于周期的概念。
1. 圆周运动的周期:
2. 单摆周期公式:
3. 近地(“贴地”)卫星速度:由 ,
, ,再代入
,再代入 ,
, 。(此公式除了关联半径为R槽内小角度摆动周期,也可以拓展到地球上无限摆长的周期)
。(此公式除了关联半径为R槽内小角度摆动周期,也可以拓展到地球上无限摆长的周期)
4. 扔出一个粉笔头,如果力气足够大,它可以变成一颗近地卫星。那么,它一圈绕地球所需的时间是多少呢?我们知道,同步卫星的周期是 24 小时,其轨道半径约为 36000 公里。根据开普勒第三定律,越靠近地球的卫星周期越短。近地卫星的周期约为 84 分钟。
Qiusir 在刚到高中部任教时的开学第一课里,讲了这样一个例子:学生就像在最内圈的1号轨道,轨道半径最小,一天上八九节课,忙忙碌碌;老师是2号轨道的卫星,半径大些,每天只上一节课;而校长则是最远的3号轨道,一年来不了一次。在这三个轨道中,学生的速度最大。如果假设三者质量相同,学生的动能也最大。那么学生的能量最大吗?校长的能量最小吗?Qiusir 话锋一转,说道:能量除了动能,还有势能。过去我们称之为“位能”。校长虽然速度最小、周期最长,但社会赋予了他特殊的位置。从能量的角度看,总能量是动能加势能。于是,校长的总能量反而是最大的。从自然界的法理出发,大人物不必像小人物那样日夜奔波,而是以一种缓慢而宏大的方式运转。我们之所以努力读书,或许正是希望将来也能成为那种“别人一辈子也见不到你一次”的人。就像波尔的氢原子模型中,轨道越高,能级越高——这和万有引力模型下的天体运动是相通的。开普勒第三定律写作 ,椭圆退化为圆,即
,椭圆退化为圆,即 。结合引力提供向心力:
。结合引力提供向心力: 可得:
可得: ,这个比例常数只与中心天体的质量有关。(知道和理解是两个层次。)
,这个比例常数只与中心天体的质量有关。(知道和理解是两个层次。)
5. qiusir叫起来一个头发很酷的女生,qiusir开玩笑说像爱因斯坦,我回到办公室和同事分享了这一个观点,大家都觉得十分贴切,我也有同样的感觉,甚至惋惜身为物理老师的我居然没有发现这个可爱的女孩与这位伟大物理学家的相似之处。弹簧振子的周期: ,振子质量越大,动的越慢,弹簧的劲度系数越大,动的越快。
,振子质量越大,动的越慢,弹簧的劲度系数越大,动的越快。
物理之难,不在理,而在物。
6. LC震荡电路的周期: 。从另外一个角度思考这个问题:对于弹簧振子:
。从另外一个角度思考这个问题:对于弹簧振子: ,对于LC震荡电路:
,对于LC震荡电路: ,化简为:
,化简为: ,二者在微分方程上十分接近,所以有相似的物理规律。
,二者在微分方程上十分接近,所以有相似的物理规律。
7. 秒摆的周期: ,其中
,其中 。(很早以前是有个秒摆的概念)
。(很早以前是有个秒摆的概念)
8. 这位女孩没有退缩,选择继续回答问题。两个小球,编号 1 和 2,悬挂在同样高度h的点上,形成圆锥摆,1 号球的摆动半径较小,2 号球的半径较大。谁的角速度大呢?  ,推出
,推出 。——与半径无关,仅与摆锤到悬点的垂直高度有关。所以,只要h 相同,1 和 2 号球的角速度也是相同的。如果做圆锥摆的两个小球3和4,半径相同,3距离悬点的高度更低,谁的角速度大呢?根据同样的公式,
。——与半径无关,仅与摆锤到悬点的垂直高度有关。所以,只要h 相同,1 和 2 号球的角速度也是相同的。如果做圆锥摆的两个小球3和4,半径相同,3距离悬点的高度更低,谁的角速度大呢?根据同样的公式, ,3号球的h更小,所以角速度更大。
,3号球的h更小,所以角速度更大。
9. “爱因斯坦”后面的一个像随时拔出刀的剑客同学:两个小球,分别放在两个向下的光滑圆锥内滑动,1 号球在锥角较小的圆锥里,2 号球在锥角较大的圆锥上。虽然两个小球的高度相同,但运动半径不同。第一种思路: (这个公式可以用前面角速度的二级结论推导,而且类比槽最高点最小速度公式便于记忆),两个小球具有相同的线速度,半径越大的小球向心加速度越小。第二种方法是把支持力等效为绳的拉力,把圆锥模型等效为圆锥摆的模型,根据
(这个公式可以用前面角速度的二级结论推导,而且类比槽最高点最小速度公式便于记忆),两个小球具有相同的线速度,半径越大的小球向心加速度越小。第二种方法是把支持力等效为绳的拉力,把圆锥模型等效为圆锥摆的模型,根据 ,半径大的h大,所以角速度更小。
,半径大的h大,所以角速度更小。
10. 浪漫的Qiusir想叫一个有女朋友的同学,一个同学恰好在那一瞬间挠头,被qiusir以举手为由叫了起来,现在回想,挠头到底是出于头痒还是出于一个年轻人的浪漫,我也不得而知。奇妙的是,与这个男生有着深刻友谊的正是“爱因斯坦”同学。爱因斯坦说过:”Any fool can know. The point is to understand.”知道,是入门;理解,才是入口。qiusir在他的小蓝书《求师得·拾年》里写过这样一句:“有一种亲密叫惺惺相惜,有一种远离叫貌合神离”。真正的亲密并非每日厮守,有时候,空间上的靠近掩盖不了精神世界的疏远。物理中讲“分离”,常常是接触却没有挤压。人与人之间也是如此,如果世界观不一样,即使坐在一起,两个人的心也是远离的,而地球与月亮始终不远不近地相伴着,它们之间,有一种静默而恒久的亲密。qiusir分享了以前的学生写过最好的情诗:“不在你左右,却被你左右”。假设地球开设了一个贯穿地心的地下铁,一趟旅程大概需要42min。这位男同学这时猛地一蹬,把自己变成一颗近地卫星从地球一端飞到另一端的时间——也是42min,而比时间更动人的是两个人的位置始终相对,在整个旅途中时刻对应,这才是物理中的浪漫,这才是旅行中的心心相印。
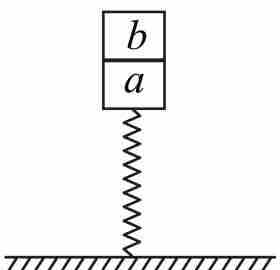
11. 质量为和的两个小球,用一根劲度系数为k 的轻弹簧连接。忽略摩擦和其他外力。求两个小球在一维平面上的运动周期。
方法一:用王聪方法画出两个小球的速度时间图像,设两个小球达到共速是弹簧的形变量为x,由图像可以看出、两个小球各自的位移大小分别为 和
和 。两个小球相对质心分别做简谐振动,等效劲度系数为
。两个小球相对质心分别做简谐振动,等效劲度系数为 ,因此小球的振动周期为
,因此小球的振动周期为 。
。
方法二:
定义两个质点的位置为, ,
, 则弹簧的伸缩量为
则弹簧的伸缩量为
。根据牛顿第二定律,两个小球分别满足: ,
, 。相对位移的二阶导为:
。相对位移的二阶导为: 。引入约化质量
。引入约化质量 ,从而系统的相对位移满足:
,从而系统的相对位移满足: ,这是简谐运动的标准形式,其振动周期为:
,这是简谐运动的标准形式,其振动周期为: 。
。
在qiusir的课上有杨利伟一天看十六次日落的伤感,也有“有一种亲密叫惺惺相惜,有一种远离叫貌合神离”的唏嘘,还有“不被你左右,却被你左右”的浪漫,物理的难不在理而在物,理是可以记,可以背的,但物是我们生活的这个大千世界,可能qiusir讲的更多的是“物”,而把“理”交给学生自己去探索,上课介绍时有句话我忘了说,“虽然只有短短四十分钟,我相信大家一定会有很多收获,可能是物理方面的,可能不止于物理”。
【下期预告】光的干涉---薄膜的奥秘
你是否曾被肥皂泡表面的绚丽色彩吸引?是否好奇油膜上的斑斓条纹从何而来?
下一期,金老师将以公开课的形式,亲手制作彩色肥皂膜,探索薄膜干涉的核心原理。
还将解锁它在科技中的神奇应用——从空气劈尖精准判断玻璃表面的平整度,到眼镜镀膜如何提升清晰度,每一处细节都蕴含着物理与生活的深度对话。
带上你的好奇心,让我们一同揭开光的艺术面纱,在理论与实践的碰撞中,共赴这场“光之盛宴”!










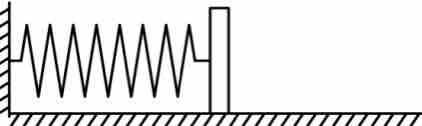 每次都把物块拉到右侧不同位置由静止释放,释放时弹力
每次都把物块拉到右侧不同位置由静止释放,释放时弹力






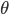


 导轨处于匀强磁场中,磁感应强度大小为
导轨处于匀强磁场中,磁感应强度大小为